Multi-agent Reinforcement Learning Notes

A simple note on the RL used in single-agent and multi-agent.

切换中文

Sequential Decision Making

• Modeling agents in sequential decision making problems, rather than just single-step or one-shot decision problems.
• Discuss a sequential decision problem in:
  • A fully observable stochastic environment
  • With a Markov transition model
  • Additive rewards Typically includes a set of states, a set of actions, a transition model, and a reward function. The solution to the problem is the policy.
• If the sequence has no time limit, and the optimal policy only depends on the state, independent of time, it is called a stationary policy.

Bellman Equation, U and Q Functions

• The value function represents the cumulative reward of a state/action sequence, such as U(s0,a0,s1,a0....), starting from the current state and action s0,a0.

• The value is defined by an additive discount, where future rewards are discounted by gamma:

  \[ U\left(\,\left[s_{0},\,s_{1},\,s_{2},\,\cdots\,\right]\,\right)=R(s_{0})+\gamma R(s_{1})+\gamma ^2 R(s_{2})+\,\cdots \]

  • Because recent rewards are more important.
  • If rewards can be invested, earlier rewards have higher value.
  • This is equivalent to each transition having a \(1-\gamma\) chance of unexpected termination.
  • Satisfies stationarity, meaning the best action at time t+1 is the same as the best action at time t in the future.
  • Prevents infinite sequence transitions.

• Based on the value function, the best action can be selected at each state, i.e., the action that maximizes the current value (instantaneous reward + expected discounted future value):

  • There is an expectation here, as each action can lead to different future states (with probability), so the value of an action is the sum of its expected value over all possible future states.

  • The value function is only a function of the state, as it has already accumulated the expectation over all actions:

    \[ \pi^*(s) = \underset{a \in A(s)}{\text{argmax}} \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma U(s^{'})] \]

• Similarly, the value function is only a function of the state, and has already accumulated the expectation over all actions. This is essentially the same as the previous formula, but without the argmax to select actions; instead, it's a max, as the agent assumes the best action is taken. The interpretation is: if the agent selects the best action, the state value is the expected reward of the next transition plus the discounted value of the next state:

  \[ U(s) = \underset{a \in A(s)}{\text{max}} \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma U(s^{'})] \]

  • Note that these two formulas are essentially the same; both involve selecting actions and summing over all possible states, but this is based on an estimate of the future expectation. The actual execution is choosing an action and transitioning to a state.
  • This equation is the Bellman Equation.

• Introduce the Q-function, which is a function of both action and state, while U is just a function of state. The relationship between them is as follows:

  \[ U(s) = \underset{a \in A(s)}{\text{max}} Q(s,a) \]

• Similarly, the Bellman equation can be written for the Q-function:

  \[ Q(s,a) = \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma Q(s^{'},a^{'})] \]

• Note that the above discussion focuses on the optimal value function and optimal Q-function, both using max, meaning they compute the return under the optimal policy, as opposed to on-policy value functions and Q-functions, which calculate the expected return.

Reward Shaping

• The reward function R can be modified (without changing the optimal policy) to stabilize the reinforcement learning process.

  • Constraints: Avoid agent exploitation of reward.
  • Exploration: Encourage exploration.
  • Acceleration: Improve sparse reward situations by breaking tasks down into smaller sub-tasks, making it easier for the agent to learn.

• A common modification is the introduction of a potential function.

• A potential function is a state-only function \(\Phi(s)\) (unlike the value function, it is independent of action/state sequences and does not result from removing actions).

• The potential function encodes the objective environmental factors that influence the rewards.

• It can be proven that a potential function can be any arbitrary function of state s, and when added to the immediate reward, the optimal policy derived from the Bellman equation remains unchanged. Specifically, when the reward function is modified as:

  \[ R^{'}(s,a,s^{'}) = R(s,a,s^{'}) + \gamma \Phi(s^{'}) - \Phi(s) \]

  The optimal policy remains unchanged, \(Q(s,a)=Q^{'}(s,a)\).

Solving MDPs

Value Iteration

• With n states, there are n equations and n unknowns in the Bellman equation. The analytical solution of nonlinear equations is difficult, but an iterative method can be used. Starting with random initial values, each state's value is updated based on neighboring states' values until equilibrium is reached.

• Introduce an iteration timestep i, the Bellman update (Bellman Update) is as follows:

  \[ U_{i+1}(s) \leftarrow \underset{a \in A(s)}{\text{max}} \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma U_i(s^{'})] \]

• It can be proven that infinite iterations will guarantee convergence to the optimal solution (assuming the immediate rewards are correct).

Policy Iteration

• Sometimes we do not need to compute the exact value function, just the action that yields the maximum value. This leads to the idea of directly iterating and optimizing the policy.

• Starting with an initial policy, the following two steps are alternated:

  • Policy Evaluation: Given a policy, compute the value of each state under the policy at a particular timestep.
  • Policy Improvement: Calculate a new policy based on the value function (using the Bellman equation) for all states.

• The process continues until policy improvement does not result in a significant change in the value function.

• Policy evaluation is also based on the Bellman equation, but we do not need to traverse actions since they are determined by the policy. By fixing the current policy \(\pi_i\) at timestep i, we obtain n equations, which can be solved:

  \[ U_{i}(s) = \sum_{s^{'}} P(s^{'}|s,\pi_i(s))[R(s,\pi_i(s),s^{'}) + \gamma U_i(s^{'})] \]

• When the state space is large, solving it exactly becomes difficult. In this case, a modified policy iteration can be used for policy evaluation, where the value function for the next timestep is computed directly from the current policy and iterated repeatedly:

  \[ U_{i+1}(s) \leftarrow \sum_{s^{'}} P(s^{'}|s,\pi_i(s))[R(s,\pi_i(s),s^{'}) + \gamma U_i(s^{'})] \]

• The above method is synchronous, meaning all states are updated at each iteration. In fact, we can update only a subset of states, which is called asynchronous policy iteration.

  • The advantage is that we can focus on updating strategies for certain effective states, as some states may not reach an optimal solution regardless of the action taken.

Linear Programming

• TBD

Online Algorithms

• Value iteration and policy iteration are offline methods: given all conditions/rewards, the optimal solution is computed, and the agent executes it.
• Online algorithms: The agent does not receive an offline solution and execute it. Instead, it computes decisions in real-time at each decision point.

Slot Machine Problem

• TBD

POMDP

• Partially Observable Markov Decision Process
• Since the agent is uncertain about its current state (the definition of partial observability), a belief state is introduced, and the agent’s decision-making cycle has an additional step:
  • Act based on the belief state.
  • Perceive observations (evidence).
  • Update the belief state based on the perception, action, and previous belief state through some updating mechanism.
• In physical state space, solving POMDP can be simplified to solving the MDP in the belief state space.
• Value iteration for POMDPs.

Single Agent RL

• The agent is in an MDP but does not know the transition model or reward function and needs to take actions to learn more information.
• The sequential decision-making problem above assumes a known environment and optimal policy derivation. However, in general reinforcement learning, the environment is unknown, and the agent learns the optimal policy through interaction with the environment.
• Model-based Methods:
  • The environment provides a transition model or initially an unknown model that needs to be learned.
  • Typically, a value function is learned, defined as the total reward accumulated from state s.
  • The sequential decision-making problems discussed above

are often solved through value iteration or policy iteration in a model-based manner. - Model-free Methods: - The environment is not known beforehand and needs to be learned. Instead of computing and using a model, the agent computes and learns the value function or policy. - Model-free approaches are often simpler to implement than model-based methods but may require more interactions with the environment. Examples: - Q-learning - SARSA - Monte Carlo methods.

Passive Reinforcement Learning

• The policy is fixed, and the value function is learned.
• The policy is fixed, for example, a greedy approach that selects the action with the maximum value. In this case, the Q-function only needs to be learned, and the optimal action under the fixed policy will emerge.
• This is similar to policy evaluation (where, given a policy, the value of each state at a particular time step is computed), but the agent doesn't know the transition probabilities between states or the immediate rewards after taking an action.

Direct Value Estimation

• The value of a state is defined as the expected total reward (reward-to-go) from that state.
• Each trial will leave a sample of the value for the states it passes through (multiple visits to the same state will provide multiple samples).
• This way, samples are collected, and supervised learning can be used to map states to values.
• However, this method ignores an important constraint: the value of a state should satisfy the Bellman equation for the fixed policy, i.e., the value of the state is related to the reward and expected value of the successor states, not just its own value.
• Ignoring this will lead to a larger search space and slow convergence.

Adaptive Dynamic Programming (ADP)

• The agent learns the transition model between states and uses dynamic programming to solve the MDP.
• In a fully observable or deterministic environment, the agent continually runs trials to gather data, then trains a supervised model that takes the current state and action as inputs and outputs the transition probabilities (the transition model).
• After obtaining the transition model, the agent can solve the MDP using sequence decision methods, correcting the policy iteratively.
• ADP requires the agent to trial continuously, gather historical data with reward signals, and then learn the environment's transition model, which transforms the problem into a known sequence decision problem.
• ADP can be seen as an extension of policy iteration in the passive reinforcement learning setting.

Temporal Difference Learning

• In the passive reinforcement learning setting, where a policy \(\pi\) is given, if the agent takes action \(\pi(s)\) from state \(s\) and transitions to state \(s^{'}\), the value function is updated using the temporal difference equation:

  \[ U^{\pi}(s) \leftarrow U^{\pi}(s) + \alpha (R(s,\pi(s),s^{'}) + \gamma U^{\pi}(s^{'}) - U^{\pi}(s)) \]

• Here, \(\alpha\) is the learning rate. Compared to Bellman, temporal difference updates the value based on the observed difference between the value of state \(s\) and the reward plus discounted future value of state \(s^{'}\):

  • The difference term provides error information, and the update reduces this error.

  • The modified formula shows that the value of the state is updated using interpolation between the current value and the reward + future discounted value:

    \[ U^{\pi}(s) \leftarrow (1-\alpha)U^{\pi}(s) + \alpha (R(s,\pi(s),s^{'}) + \gamma U^{\pi}(s^{'})) \]

• Connection and difference with adaptive dynamic programming:

  • Both adjust the current value based on future estimates, but ADP uses a weighted sum over all possible successor states, while temporal difference only uses the observed successor state.
  • ADP aims for as many adjustments as possible to ensure consistency between the value estimate and the transition model, while TD makes a single adjustment based on the observed transition.
  • TD can be seen as an approximation of ADP:
    • TD can use the transition model to generate multiple pseudo-experiences, rather than relying only on the actual observed transition, leading to value estimates that are closer to ADP.
    • Prioritized sweeping updates states that are highly probable and recently had large adjustments in their successor states.
    • One advantage of TD as an approximation of ADP is that early on, the transition model may not be accurate, so learning an exact value function to match the transition model is less meaningful.

Active Reinforcement Learning

• The policy needs to be learned.
• A complete transition model needs to be learned, taking into account all possible actions since the policy is not fixed (unknown).
• Consider whether, after learning the optimal policy, simply executing it is always the right action.

Introducing Exploration

• Adaptive dynamic programming is greedy, so exploration needs to be introduced.
• A broad design would introduce an exploration function \(f(u, n)\), where a higher value \(u\) encourages greediness, and fewer trials \(n\) encourage exploration.

TD Q-learning

• A temporal difference method for active reinforcement learning.

• No model of the transition probabilities is required (model-free method).

• The agent learns the action-value function to avoid needing the transition model itself:

  \[ Q(s,a) \leftarrow Q(s,a) + \alpha (R(s,a,s^{'}) + \gamma \max_{a^{'}}Q(s^{'},a^{'}) - Q(s,a)) \]

• No transition model \(P(s'|s,a)\) is needed.

• Since no policy is provided, we need to take the max over all possible actions.

• Learning is difficult when rewards are sparse.

Sarsa

• Sarsa stands for state, action, reward, state, action, and represents the update rule for this five-tuple:

  \[ Q(s,a) \leftarrow Q(s,a) + \alpha (R(s,a,s^{'}) + \gamma Q(s^{'},a^{'}) - Q(s,a)) \]

• Compared to TD Q-learning, it does not take the max over all possible actions, but instead updates based on the action actually taken.

• If the agent is greedy and always selects the action with the highest Q-value, then Sarsa and Q-learning are equivalent. If not greedy, Sarsa penalizes actions that encounter negative rewards during exploration.

• On/Off Policy:

  • Sarsa is on-policy: "If I stick to my policy, what is the value of this action at this state?"
  • Q-learning is off-policy: "If I stop following my current policy and instead use an estimated optimal policy, what is the value of this action at this state?"

Generalization in Reinforcement Learning

• Both the value function and the Q-function are stored in table form, and the state space is large.
• If they can be parameterized, the number of parameters to be learned can be greatly reduced.
• In passive reinforcement learning, supervised learning can be used to learn the value function based on trials, and functions or neural networks can be used to parameterize this.
• In temporal difference learning, the difference term can be parameterized and learned through gradient descent.
• There are several issues with parameterizing and approximating the value or Q-function:
  • Difficulty in convergence.
  • Catastrophic forgetting: This can be mitigated by experience replay, where trajectories are saved and replayed to ensure that value functions for states not currently visited remain accurate.
• Reward function design, how to address sparse rewards?
  • Issue: credit assignment, which action should be credited for the final positive or negative reward?
  • Reward shaping can help by providing intermediate rewards; potential functions are one example, reflecting progress towards partial goals or measurable distances from the final desired state.
• Another approach is hierarchical reinforcement learning, TBD.

Policy Search

• Adjust the policy as long as there is improvement in performance.

• A policy is a function mapping states to actions.

• If the policy is parameterized, it can be optimized. However, optimizing the Q-function doesn't necessarily lead to the optimal value estimate or Q-function because policy search only cares whether the policy is optimal.

• Directly learning Q-values and then using argmax to derive the policy can lead to discrete, non-differentiable issues. In this case, Q-values are treated as logits, and softmax is used to represent action probabilities, with techniques like Gumbel-Softmax ensuring the policy is continuously differentiable.

• If the expected reward from executing the policy can be written as a parameterized expression, policy gradient methods can be used for direct optimization. Otherwise, the expression can be computed by observing accumulated rewards during policy execution and optimized using experience gradients.

• For the simplest case where only one action is taken, the policy gradient can be written as:

  \[ \triangledown_{\theta}\sum_a R(s_0,a,s_0)\pi_{\theta}(s_0,a) \]

• This sum can be approximated using samples generated from the policy’s probability distribution, and extended to sequential states, resulting in the REINFORCE algorithm. Here, the policy probability weighted sum is approximated over N trials, and the single-step reward is extended to a value function, with states extended to the entire state space of the environment:

  \[ \frac{1}{N} \sum_{j=1}^N \frac{u_j(s) \triangledown_{\theta}\pi_{\theta}(s,a_j)}{\pi_{\theta}(s,a_j)} \]

MARL (Multi-Agent Rl)

• TBD
• 
• 
• 
• 

序列决策

• 建模序列决策下的智能体，而不仅仅是单一回合或者一次性决策问题
• 讨论一个
  • 完全可观测的随机环境
  • 具有马尔科夫转移模型
  • 加性奖励 的序列决策问题，通常包含状态集合、动作集合、转移模型、奖励函数。问题的解即策略。
• 假如序列没有时间限制，最优策略只与状态有关，与时间无关，则称最优策略是平稳的。

bellman方程，U和Q函数

• 价值函数（价值函数），代表某一状态/行为序列的奖励综合，U(s0,a0,s1,a0....)，从当前状态和动作s0,a0开始

• 用加性折扣定义价值，未来的奖励乘gamma递减:

  \[ U\left(\,\left[s_{0},\,s_{1},\,s_{2},\,\cdots\,\right]\,\right)=R(s_{0})+\gamma R(s_{1})+\gamma ^2 R(s_{2})+\,\cdots \]

  • 因为看重近期奖励
  • 如果奖励可以投资，则越早的奖励价值越大
  • 等价于每次转移有\(1-\gamma\)的意外终止
  • 满足平稳性，t+1的最佳选择未来也是t的最佳选择未来
  • 避免无穷的序列转移

• 基于价值函数，可以选出当前最佳动作，即在当前状态下，使得当前价值最大的动作（转移的即时奖励+后续的期望折扣价值）

  • 这里存在一个期望，因为每个动作都可能到每个状态（概率），因此一个动作的价值是在所有可能的未来状态下累加。

  • 价值函数只是状态的函数，已经对所有动作累加求期望

    \[ \pi^*(s) = \underset{a \in A(s)}{\text{argmax}} \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma U(s^{'})] \]

• 同理，价值函数只是状态的函数，已经对所有动作累加求期望，其实就是上式，只不过不是argmax选动作，而是max，这里的解释是：假设agent选择了最佳动作，状态价值是下一次转移的期望奖励加上下一个状态的折扣价值

  \[ U(s) = \underset{a \in A(s)}{\text{max}} \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma U(s^{'})] \]

  • 注意两个式子本质是一样的，都是挑动作，都是在所有可能的状态下累加，但这是基于对未来期望的估计，实际执行就是选择一个动作，转移到一个状态。
  • 该式即bellman方程

• 引入Q函数，Q是动作和状态的函数，U仅仅是状态的函数，两者的转换关系如下

  \[ U(s) = \underset{a \in A(s)}{\text{max}} Q(s,a) \]

• 同理也可以写成bellman方程的形式

  \[ Q(s,a) = \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma Q(s^{'},a^{'})] \]

• 注意以上讨论的都是最优价值函数和最优q函数，都是取max，即计算最优策略下的return，区别于on-policy价值函数和q函数，计算的是期望

reward shaping

• 可以通过修改奖励函数R（而不改变最优策略）来使强化学习过程更加稳定

  • 约束：避免一些agent套路reward的情况
  • 探索：鼓励explore
  • 加速：改善奖励稀疏的情况，将任务分解成更小的子任务，从而使得智能体更容易学习

• 一种常见的修改方式是引入势函数

• 势函数是一个仅与状态相关的函数\(\Phi(s)\)（不同于价值函数，与动作状态序列无关，不是消掉动作得到的）

• 势函数编码了环境本身客观存在的因素，影响了奖励

• 可以证明，势函数可以为状态s的任意函数，且加入及时奖励时，bellman方程得到的最优策略不变，即当奖励函数改成

  \[ R^{'}(s,a,s^{'}) = R(s,a,s^{'}) + \gamma \Phi(s^{'}) - \Phi(s) \]

  时，最优策略不变，\(Q(s,a)=Q^{'}(s,a)\)

求解MDP

价值迭代

• n个状态，bellman方程就有n个方程n个未知数，非线性方程的解析解很难得到，可以通过迭代的方法，随机初始值，再根据邻居的价值更新每个状态的价值，重复直至平衡

• 引入迭代的timestep i，bellman更新(Bellman Update)如下

  \[ U_{i+1}(s) \leftarrow \underset{a \in A(s)}{\text{max}} \sum_{s^{'}} P(s^{'}|s,a)[R(s,a,s^{'}) + \gamma U_i(s^{'})] \]

• 可以证明：无限次迭代可以保证达到平衡，得到最优策略(前提是即时奖励是正确的)。

策略迭代

• 有些时候我们并不需要得到精确的价值函数，只要知道哪个动作带来的价值最大即可，这就引出了直接对策略进行迭代优化的思想 .
• 从某个初始策略开始，交替进行以下两个步骤
  • 策略评估：给定策略，计算执行策略后某一时间步每个状态的价值
  • 策略改进：基于所有状态价值的一步前瞻（即价值函数bellman方程）来计算新的策略
• 直到策略改进不对价值产生（足够大）改变
• 策略评估也是基于bellman方程，只不过不用遍历动作，因为动作已经由策略决定，然后固定当前时间步i策略\(\pi_i\)，我们可以得到n个方程，求解即可

\[ U_{i}(s) = \sum_{s^{'}} P(s^{'}|s,\pi_i(s))[R(s,\pi_i(s),s^{'}) + \gamma U_i(s^{'})] \]

• 在状态空间比较大的时候，精确求解比较困难，这时候可以使用修正策略迭代来进行策略评估，即下一时间步的价值函数直接由当前策略计算出，然后反复迭代

\[ U_{i+1}(s) \leftarrow \sum_{s^{'}} P(s^{'}|s,\pi_i(s))[R(s,\pi_i(s),s^{'}) + \gamma U_i(s^{'})] \]

• 以上都是同步的形式，即每次迭代更新所有状态。事实上可以只更新部分状态，即异步策略迭代
  • 好处是可以只专注为某些有效的状态更新策略，有些状态可能无论什么动作都达不到最优解

线性规划

• TBD

在线算法

• 价值迭代和策略迭代都是离线的：给定了所有条件/奖励，先生成最优解，然后agent执行
• 在线算法：agent不是拿到离线解之后再执行，而是在每个决策点即时计算决策。

老虎机问题

• TBD

POMDP

• 部分可观测环境的马尔科夫决策过程
• 因为agent对自己所处的状态不确定（这是部分可观测的定义），所以需要引入一个信念状态，然后agent的决策周期增加了一个环节
  • 根据信念状态，执行动作
  • 观测感知（证据）
  • 基于感知、动作、之前的信念状态，通过某种更新机制得到新的信念
• 在物理空间状态上求解POMDP可以简化为在信念状态空间上求解MDP
• POMDP的价值迭代

Single Agent RL

• Agent处在MDP当中，不知道转移模型和奖励函数，需要通过采取行动了解更多信息
• 上文的序列决策是在已知环境下，如何得到一个最优策略，其实不需要agent的互动。一般而言的强化学习是指环境未知，需要agent在与环境的交互中来得到数据，从而确定最优策略。
• 基于模型的方法
  • 环境提供了转移模型，或者一开始未知环境模型，但是需要去学习
  • 通常会学习一个价值函数，定义为状态s之后的奖励总和
  • 上文的序列决策都是在基于模型的前提下阐述的
• 无模型的方法
  • 不知道环境的转移模型，而且也不会学习它
  • agent直接学习策略，一般通过两种方式来在无模型的前提下学习策略
    • 学习Q函数，即学习处于状态s下采取动作a得到的奖励
    • 直接学习策略\(\pi\)，即学习状态到动作的映射

被动强化学习

• 策略固定，学习价值函数
• 策略固定，比如说贪心的取价值最大的动作，这时候只需要将Q函数学好，策略固定的情况下具体的最优动作也就出来了。
• 类似于策略评估（给定策略，计算执行策略后某一时间步每个状态的价值），但agent不知道采取动作后到各个状态的转移概率，也不知道即时奖励

直接价值估计

• 一个状态的价值定义为从该状态出发的期望总奖励（reward-to-go）
• 每次trial都会在其经过的状态上留下一个价值的数值样本(多次经过一个状态就提供多个样本)
• 这样就收集了样本，可以使用监督学习学到状态到价值的映射
• 但是该方法忽略了一个重要约束：状态价值应满足固定策略的bellman方程，即状态的价值和后继状态的奖励和期望价值相关，而不是只取决于自己
• 这种忽略将导致搜索空间变大，收敛缓慢

自适应动态规划(ADP)

• agent学习状态之间转移模型，并用dp解决MDP
• 在环境确定/可观测的情况下，不断的trial，得到数据，训练一个监督模型，输入当前状态和动作，输出后续状态概率，即转移模型
• 得到转移模型后，之后按照序列决策的方法，通过修正策略迭代求解MDP
• 可以看到ADP是需要agent先不断的trial，在环境中得到一系列包含奖励信号的历史数据，然后用这些数据学习到环境的转移模型，将其转化为环境已知的序列决策问题。
• 自适应动态规划可以看成是策略迭代在被动强化学习设置下的扩展

时序差分学习

• 在被动强化学习的setting下，即给定策略\(\pi\)，假如在状态s下采取动作\(\pi(s)\)转移到了状态\(s^{'}\)，则通过时序差分方程更新价值函数:

  \[ U^{\pi}(s) \leftarrow U^{\pi}(s) + \alpha (R(s,\pi(s),s^{'}) + \gamma U^{\pi}(s^{'}) - U^{\pi}(s)) \]

• 其中\(\alpha\)是学习率。对比bellman，时序差分是在观测到在状态s下采取动作a到达了状态s'，就根据这个相继状态之间价值的差分更新价值:

  • 差分项是关于误差的信息，更新是为了减少这个误差

  • 公式变化后可以看出来是当前价值和奖励+未来折扣价值之间做插值:

    \[ U^{\pi}(s) \leftarrow (1-\alpha)U^{\pi}(s) + \alpha (R(s,\pi(s),s^{'}) + \gamma U^{\pi}(s^{'})) \]

• 与自适应动态规划的联系与区别：

  • 都是根据未来调整当前价值，自适应的未来是在所有可能后继状态上加权求和，而时间差分的未来是观测到的后继
  • 自适应尽可能进行多的调整，以保证价值估计和转移模型的一致性；差分对观测到的转移只做单次调整
  • TD可以看成一种近似ADP
    • 可以用转移模型生成多个pseudo experience，而不是仅仅只看真实发生的一次转移，这样TD的价值估计会接近ADP
    • prioritized sweeping，对哪些高概率 后继状态刚刚经过大调整的状态进行更新
    • TD作为近似ADP的一个优点是，训练刚开始时，转移模型往往学不正确，因此像ADP一样学习一个精确的价值函数来匹配这个转移模型意义不大。

主动强化学习

• 需要学习策略
• 需要学习一个完整的转移模型，需要考虑所有的动作，因为策略不固定（未知）
• 需要考虑，得到最优策略后，简单的执行这个策略就是正确的吗？

引入explore

• 自适应动态规划是greedy的，需要引入exploration
• 一个宏观的设计，是引入探索函数f(u,n)，选择价值u较高的即贪心，选择尝试次数n少的即探索

TD Q-learning

• 一种主动强化学习下的时序差分方法

• 无需一个学习转移概率的模型，无模型的方法

• 通过学习动作-价值函数来避免对转移模型本身的需求

  \[ Q(s,a) \leftarrow Q(s,a) + \alpha (R(s,a,s^{'}) + \gamma max_{a^{'}}Q(s^{'},a^{'}) - Q(s,a)) \]

• 不需要转移模型P(s'|s,a)

• 注意因为没有给定策略，这里需要对所有可能动作取max

• 奖励稀疏时难以学习

Sarsa

• 即state,action,reward,state,action，sarsa的缩写代表了更新的五元组

  \[ Q(s,a) \leftarrow Q(s,a) + \alpha (R(s,a,s^{'}) + \gamma Q(s^{'},a^{'}) - Q(s,a)) \]

• 相比TD Q-learning，不是对所有可能动作取max，而是先执行动作，再根据这个动作更新

• 如果agent是贪心的，总是执行q-value最大的动作，则sarse和q-learning等价；如果不是贪心，sarsa会惩罚探索时遇到的负面奖励动作

• on/off policy

  • sarsa是on-policy：“假设我坚持我自己的策略，那么这个动作在该状态下的价值是多少？”
  • q-learning是off-policy：“假设我停止使用我正在使用的任何策略，并依据估计选择最佳动作的策略开始行动，那么这个动作在改状态下的价值是多少？”

强化学习中的泛化

• 价值函数和Q函数都用表格的形式记录，状态空间巨大
• 要是能参数化，需要学习的参数值可以减少很多
• 对于被动强化学习，需要根据trials使用监督学习价值函数，这里可以用函数或者NN来参数化。
• 对于时序差分学习，可以将差分项参数化，通过梯度下降学习
• 参数化来近似学习价值或者q函数存在几个问题
  • 难以收敛
  • 灾难性遗忘：可以通过experience replay，保存轨迹进行回放，确保agent不再访问的那部分状态空间上的价值函数仍然准确
• 奖励函数设计，如何解决稀疏奖励？
  • 问题：credit assignment，最后的正面或者负面奖励应该归因到哪次动作上
  • 可以通过修改奖励函数（reward shaping）来提供一些中间奖励，势函数就是一个例子，势反映了我们所希望的部分状态（某个子目标的实现、离最终希望的终止状态的某种可度量的距离）
• 另一种方案是分层强化学习，TBD

策略搜索

• 只要策略的表现有所改进，就继续调整策略

• 策略是一个状态到动作的映射函数

• 将策略参数化表达，尽管可以通过优化q函数得到，但并不一定得到最优的q函数或者价值估计，因为策略搜索只在乎策略是否最优

• 直接学习Q值，然后argmax Q值得到策略会存在离散不可导问题，这时将Q值作为logits，用softmax表示动作概率，用类似gumbel-softmax使得策略连续可导

• 假如执行策略所得到的期望奖励可以写成关于参数的表达式，则可以使用策略梯度直接优化；否则可以通过执行策略观测累计的奖励来计算表达式，通过经验梯度优化

• 考虑最简单的只有一次动作的情况，策略梯度可以写成下式，即对各个动作的奖励按其策略概率加权求和，并对策略参数求导。

  \[ \triangledown_{\theta}\sum_aR(s_0,a,s_0)\pi_{\theta}(s_0,a) \]

• 将这个求和用策略所定义的概率分布生成的样本来近似，并且扩展到时序状态，就得到了REINFORCE算法，这里用N次trial近似策略概率加权求和，并且将单步奖励扩展到价值函数，状态也扩展到整个环境的状态集合：

  \[ \frac1N \sum_{j=1}^N\frac{u_j(s)\triangledown_{\theta}\pi_{\theta}(s,a_j)}{\pi_{\theta}(s,a_j)} \]

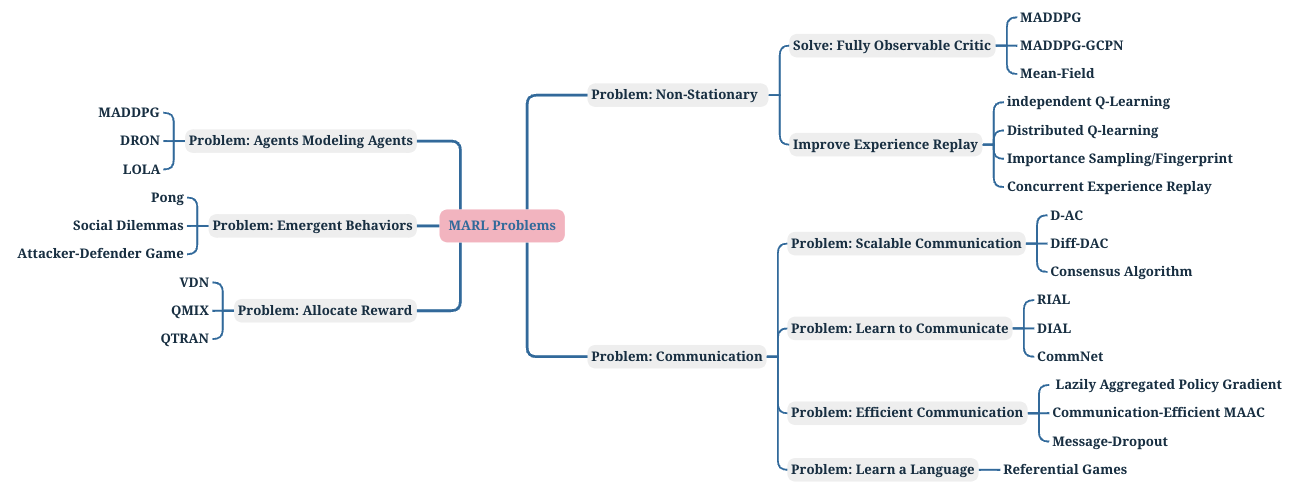
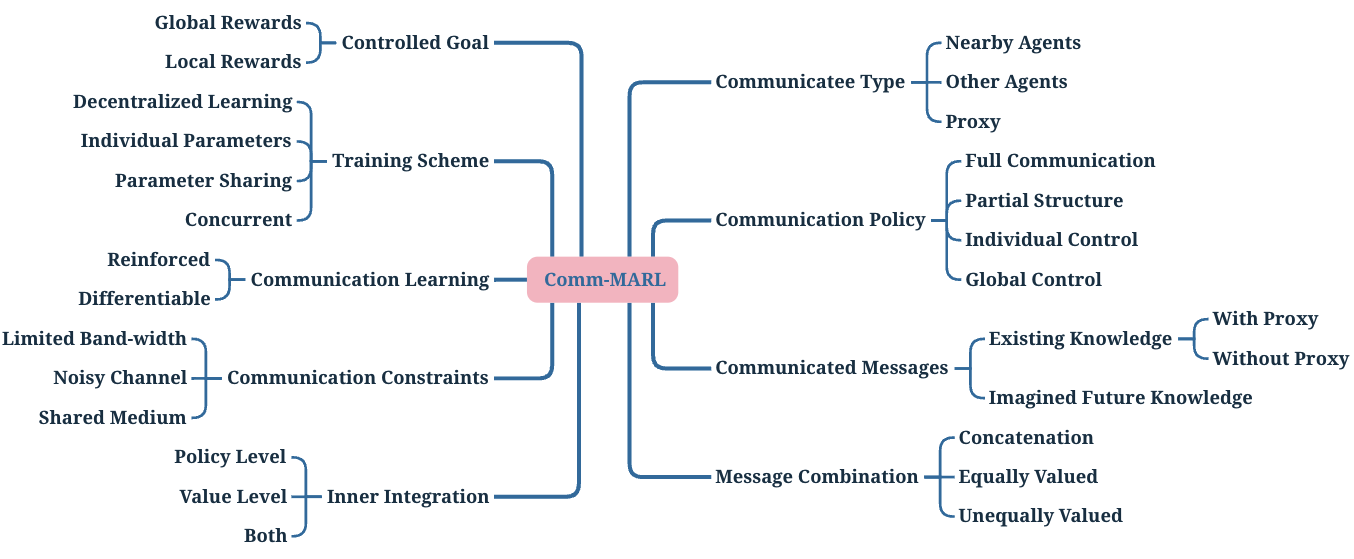
MARL (Multi-Agent Rl)

• 先挖坑
• 
• 
• 
•