Statistical Learning - A hand-write note

The ten major algorithms of statistical learning methods have been simplified and handwritten out (although I think the book itself is already quite concise). Now there is only the process of the algorithms themselves; in the future, if I have any new understandings, I will supplement them. The writing is ugly, even I can't bear to look at it, so I post it purely as a backup
Abstract

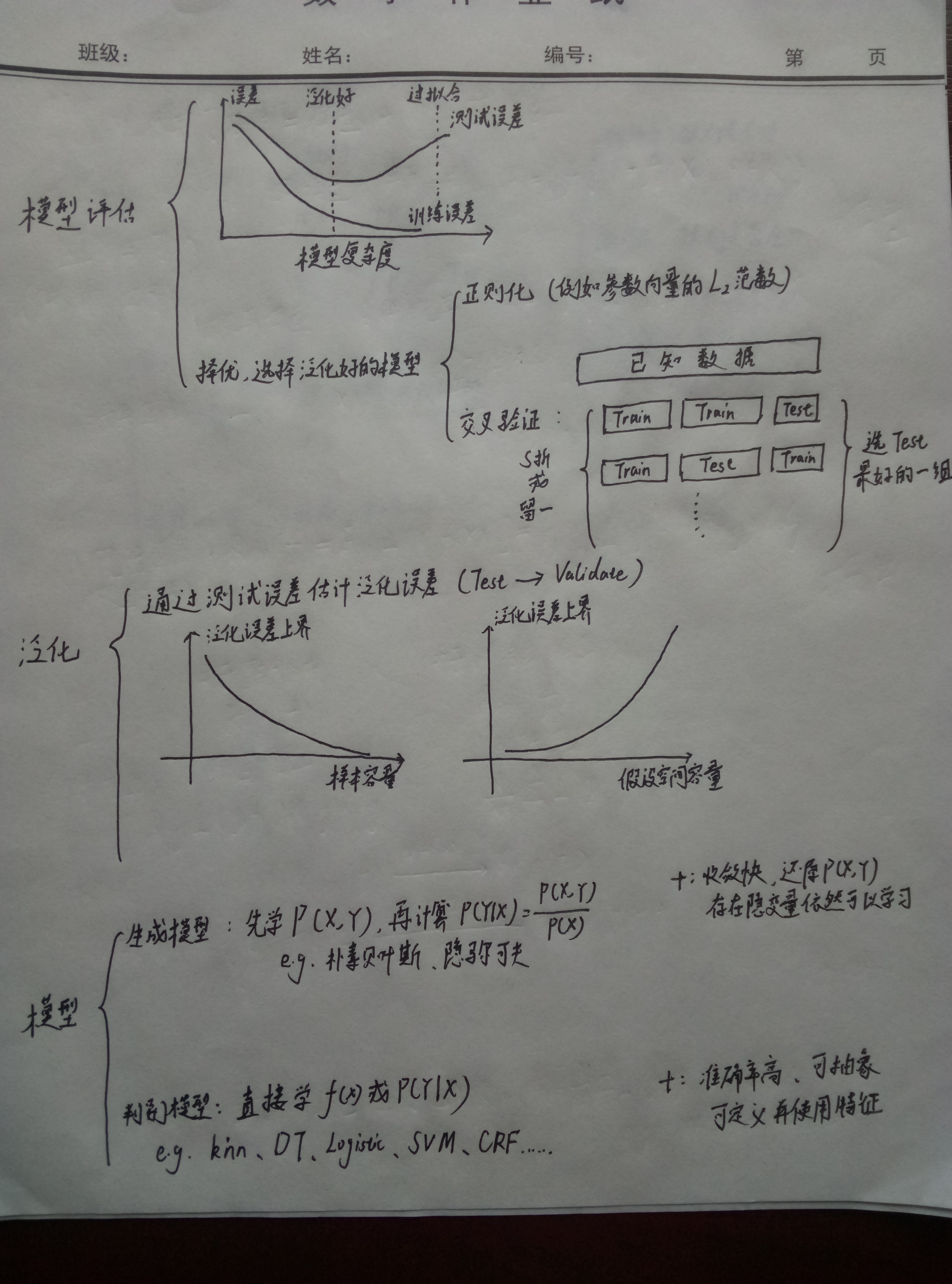

Perceptron


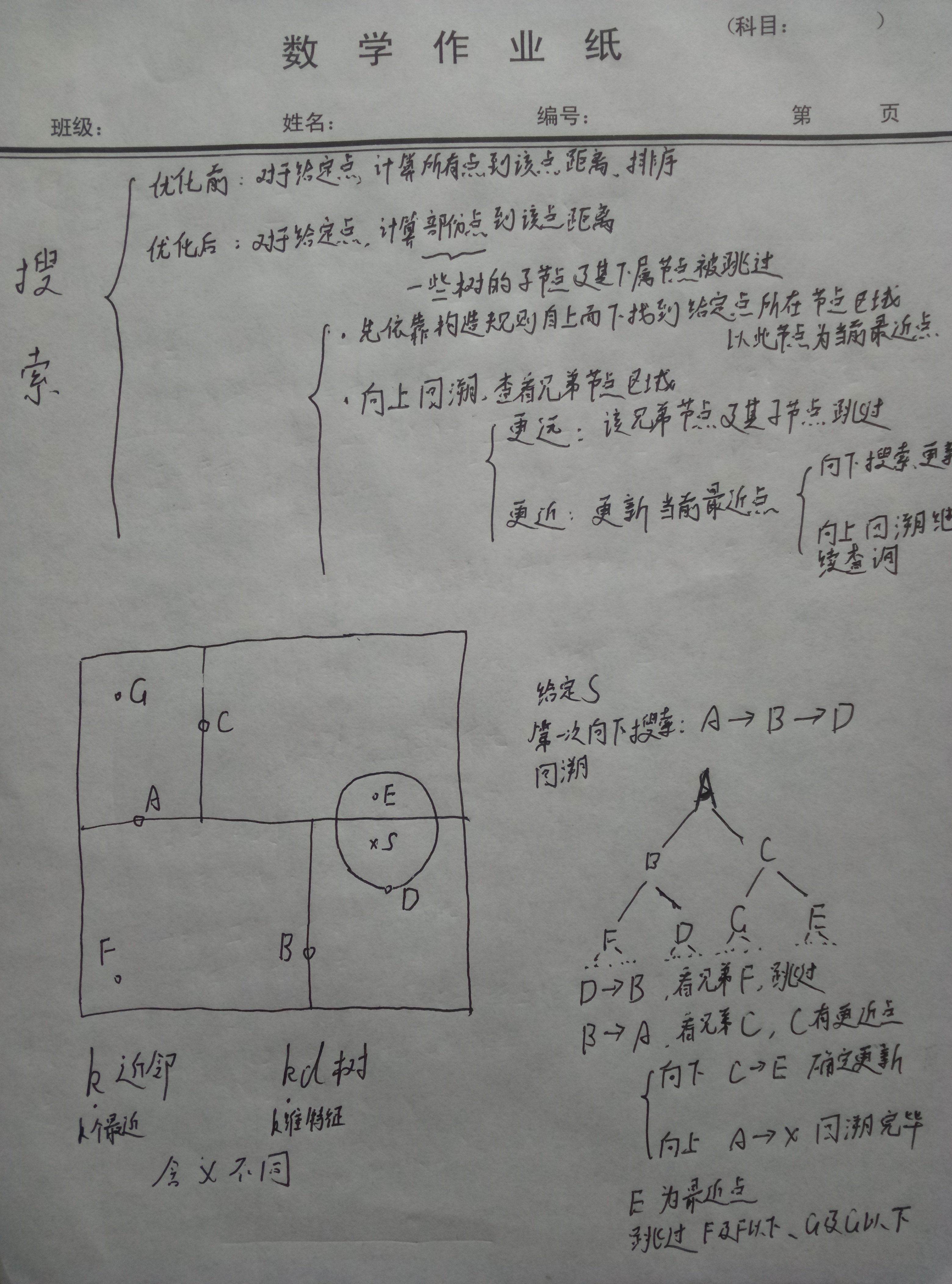
k-Nearest Neighbors

Naive Bayes

Decision Tree
- GBDT is written in the improvement method, and it is also possible
to expand and look at random forests, which is an bootstrap method that
utilizes decision trees.
![i0HzAH.jpg]()



Logistic regression, maximum entropy
- The mutual derivation between maximum entropy and logistic
regression is to be supplemented
![i0bigP.jpg]()

Support Vector Machine






Enhancement Methods
- XGBoost
![i0bn4s.jpg]()

Expectation-Maximization (EM) algorithm


- When performing inference on Gaussian mixture models using the EM algorithm, the parameters to be inferred include the mean, variance, and proportion coefficient of k Gaussian models. The latent variable represents the probability that the jth observation sample belongs to the kth Gaussian model, referred to as responsibility, while \(n_k\) is the sum of the responsibility of the kth Gaussian model over all samples, divided by \(N\) , which is used to update the GMM proportion coefficient with its mean. The mean is updated using responsibility-weighted samples, and the variance is updated in a similar manner.
- After updating the parameters, recalculate responsibility with these parameters, recalculate the E-step, and then proceed to the M-step, thereby completing the iteration.
Hidden Markov




Conditional Random Field
- Address the solutions for three types of problems, as conditional
random fields are the conditional extension of the hidden Markov model,
and the algorithms are similar
![i0bYE4.jpg]()



