Note for Latent Dirichlet Allocation

---

Latent Dirichlet Allocation Document Topic Generation Model Study Notes This article mainly summarizes from "Mathematical Curiosities of LDA(LDA数学八卦)," which is written very beautifully (recommend reading the original first). There are many places that spark further thought, and this article sorts out the steps to derive LDA, removes some irrelevant extensions, and summarizes LDA in plain language.

i0oNlT.jpg

切换中文

What is LDA used for

• LDA is a topic model; the question is actually what is a topic model used for? It is used to represent documents. Here, documents are viewed as a bag of words.
• If each word in the dictionary is considered a feature and the tfidf value is used as the magnitude of the feature to represent a document, then the feature vector of the document is too sparse and has too high a dimensionality
• The solution of LSI is to perform singular value decomposition on the document-word matrix, reduce dimensions, but the reduced dimension space obtained, i.e., the latent variables between words and documents, is unexplainable; a purely mathematical method, too forceful
• PLSA proposes that latent variables should be topics, which can represent documents as topic vectors, and define topics as a certain polynomial distribution on the dictionary. This way, PLSA contains two layers of polynomial distributions: the polynomial distribution from documents to topics (the mixing proportion of various topics in a document, i.e., the feature vector of the document), and the polynomial distribution from topics to words (the probability distribution over the entire dictionary, representing the probability of each word appearing under different topics)
• LDA specifies Dirichlet priors for the parameters of these two polynomial distributions, introducing a Bayesian framework for PLSA

Bayesian model

• LDA is a Bayesian model

• Given the training data, how does a Bayesian model learn parameters (the distribution of parameters): Bayesian estimation

  • Prior distribution for the parameter \(p(\theta)\)

  • Given the data, calculate the likelihood \(p(X|\theta)\) and evidence \(P(X)\) , and then compute the posterior distribution of the parameters according to Bayes' formula

  • Posterior distribution is the distribution of the learned parameters

    \[ p(\vartheta | X)=\frac{p(X | \vartheta) \cdot p(\vartheta)}{p(\mathcal{X})} \]

• The data may be too much, so update in batches; the posterior obtained after the last update serves as the prior for the next update, similar to the idea in stochastic gradient descent

• For the likelihood of new data, unlike maximum likelihood estimation or maximum a posteriori estimation, both of which are point estimates, directly calculating \(p(x_{new}|\theta _{ML})\) , \(p(x_{new}|\theta _{MAP})\) , Bayesian estimation requires integrating over the parameter distribution:

  \[ \begin{aligned} p(\tilde{x} | X) &=\int_{\vartheta \in \Theta} p(\tilde{x} | \vartheta) p(\vartheta | X) \mathrm{d} \vartheta \\ &=\int_{\vartheta \in \Theta} p(\tilde{x} | \vartheta) \frac{p(X | \vartheta) p(\vartheta)}{p(X)} \mathrm{d} \vartheta \end{aligned} \]

• Two issues often arise in Bayesian estimation

  • With prior knowledge and likelihood, the calculated posterior is complex
  • evidence is hard to calculate

• Therefore, conjugate and Gibbs sampling respectively solve these two problems

  • Conjugate: Given the likelihood, find a prior such that the posterior has the same form as the prior
  • gibbs sampling: Using the idea of MCMC to approximate the posterior without explicit computation of the evidence

• If it is a Bayesian model with latent variables, then there is

  \[ p(\vartheta|x) = \int_{z} p(\vartheta|z)p(z|x) \]

• In LDA, the latent variable z represents the topic to which a word belongs (the word's topic assignment), so \(p(\vartheta|z)\) is naturally easy to calculate, and then the remaining \(p(z|x)\) can be calculated using the formula for Bayesian inference:

  \[ p(z | X)=\frac{p(X | z) \cdot p(z)}{p(\mathcal{X})} \]

• Before introducing LDA, two other models are introduced: the Bayesian unigram and PLSA. The former can be considered as LDA without a topic layer, and the latter as LDA without Bayesian regularization

• Next, we will separately introduce conjugate, Gibbs sampling, Bayesian unigram/PLSA, and finally, LDA

Conjugation

Gamma function

• Definition

  \[ \Gamma (x) = \int _0 ^{\infty} t^{x-1} e^{-t} dt \]

• Due to its recursive nature \(\Gamma(x+1)=x\Gamma(x)\) , the definition of factorial can be extended to the real number domain, thereby extending the definition of the derivative of a function to the real set, for example, calculating the second derivative at 1/2

• Bohr-Mullerup theorem: If \(f:(0,\infty) \rightarrow (0,\infty)\) and satisfy

  • \(f(1)=1\)
  • \(f(x+1)=xf(x)\)
  • If \(log f(x)\) is a convex function, then \(f(x)=\Gamma(x)\)

• Digamma function

  \[ \psi (x)=\frac{d log \Gamma(x)}{dx} \]

  It has the following properties

  \[ \psi (x+1)=\psi (x)+\frac 1x \]

• The result of inferring LDA using variational inference is in the form of the digamma function

Gamma distribution

• Transform the above equation

  \[ \int _0 ^{\infty} \frac{x^{\alpha -1}e^{-x}}{\Gamma(\alpha)}dx = 1 \]

  Therefore, it is advisable to take the function in the integral as the probability density, obtaining the density function of the simplest form of the Gamma distribution:

  \[ Gamma_{\alpha}(x)=\frac{x^{\alpha -1}e^{-x}}{\Gamma(\alpha)} \]

• Exponential distribution and \(\chi ^2\) distribution are both special cases of the Gamma distribution, and they are very useful as prior distributions, widely applied in Bayesian analysis.

• Gamma distribution and Poisson distribution have a formal consistency, and in their usual representations, there is only a difference of 1 in the parameters. As previously mentioned, factorials can be represented by the Gamma function, therefore, it can be intuitively considered that the Gamma distribution is a continuous version of the Poisson distribution over the set of positive real numbers.

  \[ Poisson(X=k|\lambda)=\frac{\lambda ^k e^{-\lambda}}{k!} \]

• The limit distribution of the binomial distribution with \(np=\lambda\) is the Poisson distribution as n approaches infinity and p approaches 0. A common example used to explain the Poisson distribution is the reception of calls by a switch. Assuming the entire time is divided into several time intervals, with at most one call per interval, the probability being p, the total number of calls follows a binomial distribution. When np is a constant \(\lambda\) , dividing time into an infinite number of segments, which are almost continuous, substituting \(p=\frac{\lambda}{n}\) into the binomial distribution, taking the limit yields the Poisson distribution. On this basis, by making the distribution values continuous (i.e., replacing the factorial of k in the Poisson distribution with the Gamma function) we obtain the Gamma distribution.

Beta distribution

• Background:

  • How to obtain the distribution of the kth order statistic \(p=x_k\) when n random variables uniformly distributed in the interval [0,1] are sorted in ascending order?

  • To obtain the distribution, by employing the idea of limits, we calculate the probability that this variable falls within a small interval \(x \leq X_{k} \leq x+\Delta x\)

  • Divide the entire interval into three parts: before the small interval, the small interval, and after the small interval. If only the k-th largest number is present in the small interval, then there should be k-1 numbers before the small interval, and n-k numbers after the small interval. The probability of this situation is

    \[ \begin{aligned} P(E)&=x^{k-1}(1-x-\Delta x)^{n-k}\Delta x \\ &=x^{k-1}(1-x)^{n-k}\Delta x+\omicron (\Delta x) \\ \end{aligned} \]

  • If there are two or more numbers within a small interval, the probability of this situation is \(\omicron (\Delta x)\) , therefore, only consider the case where there is only the k-th largest number within the small interval. In this case, let \(\Delta x\) tend towards 0, then we obtain the probability density function of the k-th largest number (note that the coefficient of event E should be \(nC_n^k\) ):

    \[ f(x)=\frac{n!}{(k-1)!(n-k)!}x^{k-1}(1-x)^{n-k} \quad x \in [0,1] \]

    Expressed in terms of the Gamma function (let \(\alpha =k,\beta = n-k+1\) ), we obtain:

    \[ \begin{aligned} f(x)&=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1} \\ &=Beta(p|k,n-k+1) \\ &=Beta(\alpha,\beta) \\ \end{aligned} \]

    This is the Beta distribution; we can take the point of the maximum probability distribution as the predicted value for the kth largest number.

• Beta distribution is actually a prediction of a distribution, that is, the distribution of distributions. In the background, we are looking for the probability distribution of the kth largest order statistic, and we denote this kth largest order statistic as p. Now, we know there are n values uniformly distributed in the interval [0,1], and n and k establish a relative position within the interval [0,1], which is the role of \(\alpha\) and \(\beta\) (because \(\alpha\) and \(\beta\) are calculated from n and k), representing where I tend to believe p is within [0,1]. Since the n statistics are uniformly distributed and p is the kth largest among them, p tends to be at the position \(\frac kn\) .
• Therefore, the parameters of the Beta distribution ( \(\alpha\) and \(\beta\) ) are clearly meaningful, representing my prior belief about the possible location of p, even when I know nothing, that is, the prior. The result of the Beta distribution is the distribution of p calculated under this prior influence, and the actual meaning of this p is the parameter of the binomial distribution. Therefore, the Beta distribution can serve as a prior for the parameters of the binomial distribution.

Beta-Binomial conjugate

• We can establish a Beta distribution prior for the kth largest number. If we now know there are m numbers uniformly distributed between [0,1], and some of them are larger than the kth largest number while others are smaller, we can incorporate this as additional data knowledge to form the posterior distribution.
• Assuming the number to be guessed is \(p=X_k\) , now we know that there are \(m_1\) numbers smaller than \(p\) , and \(m_2\) numbers larger than \(p\) , it is obvious that the probability density function of \(p\) becomes \(Beta(p|k+m_1,n-k+1+m_2)\)
• The knowledge of m numbers added into the data is equivalent to conducting m Bernoulli experiments, because the range we are discussing is on [0,1], and the m numbers only care whether they are larger or smaller than \(p\) , the value of \(p=X_k\) can represent this probability, therefore \(m_1\) follows a binomial distribution \(B(m,p)\)

A priori	Data Knowledge	Posterior
Beta distribution	Binomial distribution	Beta distribution

• Therefore, we can obtain the Beta-Binomial conjugate

  \[ Beta(p|\alpha,\beta)+BinomCount(m_1,m_2)=Beta(p|\alpha+m_1,\beta+m_2) \]

  When the data conforms to a binomial distribution, both the prior distribution and the posterior distribution of the parameters can maintain the form of a Beta distribution. We can assign a clear physical meaning to the parameters in the prior distribution and extend this interpretation to the posterior distribution, therefore, the parameters \(\alpha,\beta\) in the Beta distribution are generally referred to as pseudo-counts, representing physical counts.

• It can be verified that when both parameters of the Beta distribution are 1, it becomes a uniform distribution. At this point, the conjugate relationship can be considered as follows: Initially, the unevenness of the coin is unknown, and it is assumed that the probability of the coin landing on heads is uniformly distributed. After tossing the coin m times, data is obtained with \(m_1\) tosses landing on heads and the rest landing on tails. By calculating the posterior probability using Bayes' formula, the probability of the coin landing on heads can be determined to be exactly \(Beta(p|m_1+1,m_2+1)\)

• Through this conjugation, we can derive an important formula concerning the binomial distribution:

  \[ P(C \leq k) = \frac{n!}{k!(n-k-1)!}\int _p ^1 t^k(1-t)^{n-k-1}dt \quad C \sim B(n,p) \]

  The following can now be proven:

  • The left side of the formula is the probability cumulative of the binomial distribution, and the right side is the probability integral of the \(Beta(t|k+1,n-k)\) distribution

  • Select n random variables uniformly distributed in [0,1], for the binomial distribution \(B(n,p)\) , if the number is less than \(p\) , it is considered successful; otherwise, it is a failure. The number of random variables less than \(p\) is C and follows the binomial distribution \(B(n,p)\)

  • At this point, we obtain \(P(C \leq k)=P(X_{k+1}>p)\) , which means that there are \(k\) variables less than \(p\) after n random variables are arranged in order

  • At this point, utilizing our probability density of the k-th largest number, we calculate it to be a Beta distribution, and then substitute it into the equation

    \[ \begin{aligned} P(C \leq k) &=P(X_{k+1} > p) \\ &=\int _p ^1 Beta(t|k+1,n-k)dt \\ &=\frac{n!}{k!(n-k-1)!}\int _p ^1 t^k(1-t)^{n-k-1}dt \\ \end{aligned} \]

    Proof by construction

• By taking the limit of n to infinity in this formula and converting it to a Poisson distribution, the Gamma distribution can be derived.

• In this section, we introduced other information to the prior, that is, there are several numbers larger and smaller than the k-th largest number. This information is equivalent to telling me: I can modify the prior of p; the position I previously tended to believe in has shifted. If I know several numbers are larger than p, then the prior position of p should be shifted to the right. If I know several numbers are smaller than p, then the prior position of p should be shifted to the left. What if I simultaneously know 100 numbers are larger than p and 100 numbers are smaller than p? The position of p remains unchanged, but I am more confident that the true position of p is now this prior position. Therefore, the Beta distribution is more concentrated at this prior position. This point will be seen again in the subsequent analysis of the meaning of the Dirichlet parameters. After adding prior knowledge and data, we form the posterior, which is the basic content of Bayes' formula.

Dirichlet-Multinomial Conjugacy

• How should we calculate the joint distribution of guessing two numbers \(x_{k_1},x_{k_1+k_2}\) ?

• Similarly, we set two extremely small intervals \(\Delta x\) , dividing the entire interval into five parts, with the extremely small intervals being \(x_1,x_2,x_3\) , after which the calculation can be obtained

  \[ f(x_1,x_2,x_3)=\frac{\Gamma(n+1)}{\Gamma(k_1)\Gamma(k_2)\Gamma(n-k_1-k_2+1)}x_1^{k_1-1}x_2^{k_2-1}x_3^{n-k_1-k_2} \]

• Organize it and it can be written as

  \[ f(x_1,x_2,x_3)=\frac{\Gamma(\alpha _1+\alpha _2+\alpha _3)}{\Gamma(\alpha _1)\Gamma(\alpha _2)\Gamma(\alpha _3)}x_1^{\alpha _1-1}x_2^{\alpha _2-1}x_3^{\alpha _3-1} \]

  This is the 3D form of the Dirichlet distribution. The \(x_1,x_2,x_3\) (which actually only has two variables) determines the joint distribution of two order statistics, and \(f\) represents the probability density.

• Observing that under the condition of \(\alpha\) being determined, the preceding series of gamma functions are actually the denominator of the probability normalization, in the following text we will express the Dirichlet distribution in a more general form:

  \[ Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow})=\frac{1}{\int \prod_{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow}} \prod_{k=1}^V p_k^{\alpha _k -1} \]

• The normalization denominator, that is, the entire set of gammas, is made to be:

  \[ \Delta(\mathop{\alpha}^{\rightarrow})=\int \prod _{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow} \]

• 参数

  \[ Dir(p|\alpha)+MultCount(m)=Dir(p|\alpha+m) \]

  The parameters in the above formula are all vectors, corresponding to the multi-dimensional case.

• Whether it is the Beta distribution or the Dirichlet distribution, they both possess an important property, that is, their mean can be represented by the ratio of the parameters, for example, for the Beta distribution, \(E(p)=\frac{\alpha}{\alpha+\beta}\) , and for the Dirichlet distribution, the mean is a vector corresponding to the vector composed of the ratios of the parameters.

Dirichlet analysis

• According to the properties of Dirichlet, the ratio of its parameters represents a partition on [0,1], determining the locations of high probability in the Dirichlet distribution, and the magnitude of the parameters determines the proportion of high probability (steepness), as shown in the following figure, the polynomial distribution has three terms with parameters \(p_1,p_2,p_3\) , their sum is 1 and each is greater than zero, and in three-dimensional space it forms a triangular face, with each point on the surface representing a polynomial distribution; the red area has a high probability, and the blue area has a low probability:

i0orkR.png

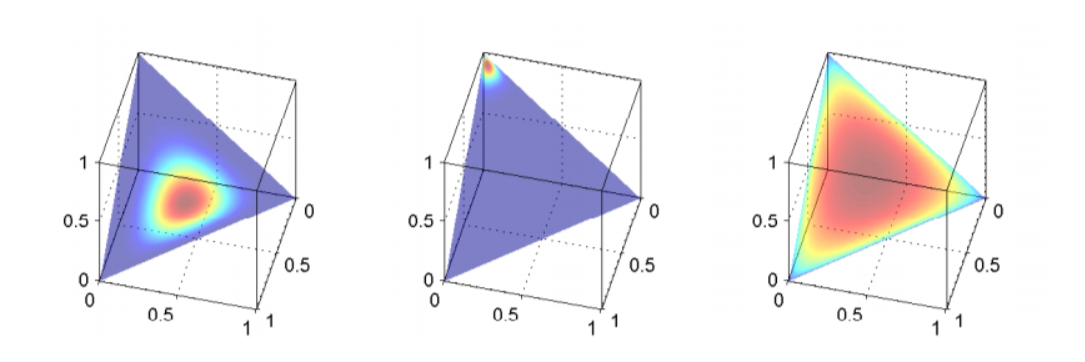
• Controlled the mean shape and sparsity of polynomial distribution parameters.
• On the far left, the three parameters \(\alpha _1,\alpha _2,\alpha _3\) of Dirichlet are equal, indicating that the red region is centered, and the values of the three \(\alpha\) are all relatively large, with a smaller red region. If the heatmap is viewed as a contour plot, this would represent a steeper red region, suggesting that Dirichlet is very confident that the parameters of the polynomial distribution will be centered. For the parameters \(p_1,p_2,p_3\) of the three polynomial distributions, a larger possibility is that all three p values are equal.
• The middle figure, with three \(\alpha\) not equal, one \(\alpha\) being larger, causing the red area to lean towards one corner of the triangular face, leading to a larger p value for one and a higher probability of smaller p values for the other two. At this point, the parameter prior acts as a concentration parameter, focusing the probability attention on certain terms.
• On the far right, like the far left, the three \(\alpha\) are equal, the red area is centered, but the values of \(\alpha\) are all smaller, causing the red area to diverge, that is, Dirichlet believes that the three p values should be in the center, but is not very certain. The result is that there is a difference between the three p values, but the difference will not be too great (still near the center), and there will not be a very steep situation (the steepest is the infinite height at the center, with a probability of 1, so the three p values must be the same).
• The ratio of \(\alpha\) determines the location of high probability in the polynomial distribution, which mainly determines the proportions of various \(p\) , setting the concentration, while the size of \(\alpha\) determines the concentration of this location; the smaller \(\alpha\) , the more concentrated the location, the more certain the distribution of p, whereas the distribution of p is roughly determined by the position of the red area, but with a larger range of variation.
• When \(\alpha\) is much smaller than 1, the Dirichlet distribution approaches another extreme. In the example of the triangular face, the red region remains steep, but the steepness is at the three corners of the triangle. It can be imagined that \(alpha\) changes from large to 1 and then decreases, with the high-probability density region gradually spreading from the center to the entire face and then concentrating at the three corners.
• Intuitive Interpretations of the Parameters The concentration parameter Dirichlet distributions are very often used as prior distributions in Bayesian inference. The simplest and perhaps most common type of Dirichlet prior is the symmetric Dirichlet distribution, where all parameters are equal. This corresponds to the case where you have no prior information to favor one component over any other. As described above, the single value α to which all parameters are set is called the concentration parameter. If the sample space of the Dirichlet distribution is interpreted as a discrete probability distribution, then intuitively the concentration parameter can be thought of as determining how "concentrated" the probability mass of a sample from a Dirichlet distribution is likely to be. With a value much less than 1, the mass will be highly concentrated in a few components, and all the rest will have almost no mass. With a value much greater than 1, the mass will be dispersed almost equally among all the components. See the article on the concentration parameter for further discussion.
• When \(\alpha\) is much smaller than 1, the probability density will mainly accumulate on one or a few terms, that is, the red area is concentrated at the three corners. In this case, the polynomial distribution obtained from Dirichlet distribution sampling is likely to be at the corners, that is, the probability density accumulates on one term, and the probabilities of the other two terms are approximately 0. When \(\alpha\) is much larger than 1, the probability density will be dispersed to various parts, which corresponds to the leftmost figure in the three figures, and the possibility of the probabilities of the three terms being relatively similar is greater.

Role in LDA

• Summarizing conjugacy: Given a distribution A, the parameter distribution of A (or the distribution of the distribution) is B. If the posterior of B, obtained after knowledge of A's data, belongs to the same class of distribution as the prior, then A and B are conjugate, and B is called the parameter conjugate distribution of A (or the prior conjugate). In the example mentioned above, the Beta distribution is the parameter conjugate distribution of the binomial distribution, and the Dirichlet distribution is the parameter conjugate distribution of the multinomial distribution.
• LDA actually models text generation as a probabilistic generative model, specifically a three-layer Bayesian model, and assumes that the parameters of both the document-topic and topic-word multinomial distributions are prior Dirichlet distributions, using Dirichlet-Multinomial conjugacy to update its posterior with data knowledge.
• To introduce the Dirichlet-Multinomial conjugacy, it is first necessary to introduce the Gamma function and its distribution. The Gamma function extends the factorial to the real number domain. After that, the Beta function, which can estimate the distribution, is introduced. With the introduction of the Gamma function, the parameters of the Beta distribution can be extended to the real number domain. Then, the Beta-Binomial conjugacy is introduced, which brings the benefit that the form of the posterior distribution is known when correcting with data. By extending this conjugacy relationship to higher dimensions (estimating multiple distributions), the Dirichlet-Multinomial conjugacy is obtained.
• The benefit of adding Dirichlet distribution as a prior for the document-to-topic and topic-to-word polynomial distributions is that by treating polynomial parameters as variables, prior information guides the range of parameter variation rather than specific values, making the model's generalization ability stronger within small training samples.
• The size of \(\alpha\) in the Dirichlet Process reflects the degree of granularity when fitting the Base Measure with the Dirichlet distribution; the larger \(\alpha\) , the less granular, and each term receives a fairly similar probability.
• The degree of dispersion corresponds to the LDA model, representing whether the document is concentrated on a few topics or distributed relatively evenly across all topics, or whether the topics are concentrated on a few words or distributed relatively evenly across the entire vocabulary.

Gibbs Sampling

Random Simulation

• Monte Carlo method, used for known distributions, involves generating a series of random samples that satisfy this distribution and using the statistics of these samples to estimate some parameters of the original distribution that are not easily analytically computed.
• Markov refers to a method of generating random samples where the process depends on the properties of Markov chains. By constructing the transition matrix of the Markov chain, it is possible to produce a sequence of samples that satisfy a given distribution when the Markov chain converges.
• A method of MCMC is random sampling, which calculates the acceptance rate using the known distribution and only accepts a portion of the samples. Gibbs sampling is an MCMC method with an acceptance rate of 1. It improves the acceptance rate but extends the sampling process.

Mars Chain

• Markov chain refers to a state transition where the probability depends only on the previous state
• Because the transition probability only depends on the previous state, the state transition probabilities can be written as a transition probability matrix. The probability distribution of each state after n transitions is the result obtained by multiplying the initial state probability distribution vector by the nth power of the matrix
• The matrix power remains constant after a certain number of iterations, meaning each row converges to the same probability distribution, and the initial probability transition also converges to the same distribution after sufficient iterations
• On the Definition of the Convergence of Markov Chains
  • If a non-periodic Markov chain has a transition probability matrix P (which may have infinitely many states), and any two states are connected (any two states can be reached through a finite number of transitions), then \(lim_{n \rightarrow \infty}P_{ij}^n\) exists and is independent of \(i\) , and this convergent matrix is denoted as \(\pi(j)\)
  • \(\pi (j)=\sum _{i=0}^{\infty} \pi (i) P_{ij}\)
  • \(\pi\) is the unique non-negative solution of equation \(\pi P = \pi\)
  • Stable Distribution Called the Markov Chain

Markov Chain Monte Carlo

• Returning to random generation, for a given probability distribution, we hope to generate the corresponding samples. An idea is to construct a Markov chain whose stationary distribution is exactly this probability distribution: because when the Markov chain converges, its stationary distribution is the probability distribution of each state. After convergence, regardless of how long a state sequence is generated through state transitions, the distribution of states in this sequence maintains the stationary distribution. If the stationary distribution is the probability distribution to be generated, then the state sequence is a random sample sequence under the given probability distribution.

• Therefore, the issue is how to construct the state transition matrix of a Markov chain given a stationary distribution. It mainly utilizes the detailed stationary condition of non-periodic Markov chains: if \(\pi(i)P_{ij}=\pi(j)P_{ij} \quad for \quad all \quad i,j\) , then \(\pi(x)\) is the stationary distribution of the Markov chain. A physical interpretation of this theorem is: if the probability mass of state i is stable, then the probability mass of the change from state i to state j is exactly complementary to the probability mass of the change from state j to state i.

• The probability of transitioning from state i to state j is denoted as \(q(i,j)\) . If \(p(i)q(i,j)=p(j)q(j,i)\) , then \(p(x)\) is the stationary distribution of this Markov chain, and the transition matrix does not need to be changed. However, in general, your luck is not that good. In the case of knowing \(p(x)\) , we need to modify \(q\) . To do this, we multiply by an acceptance rate \(\alpha\) , so that:

  \[ p(i)q(i,j)\alpha (i,j)=p(j)q(j,i)\alpha (j,i) \]

  Why is it called the acceptance rate? Because it can be understood that this \(\alpha\) is multiplied by a probability after the original state transition, representing whether this transition is accepted.

• How to determine the acceptance rate? In fact, it is self-evident \(\alpha (i,j)=p(j)q(j,i)\) , symmetric construction will suffice.

• Therefore, after each transition, we sample a variable from a uniform distribution, and if the variable is less than the acceptance rate, we transition according to the original transition matrix; otherwise, we do not transition.

• Such MCMC sampling algorithms have a problem: we actually did not modify the original transition probability matrix q, but calculated the acceptance rate based on q to ensure convergence to p. However, the acceptance rate may be calculated to be very small, leading to the state remaining stationary for a long time and slow convergence. In fact, multiplying both sides of the formula \(p(i)q(i,j)\alpha (i,j)=p(j)q(j,i)\alpha(j,i)\) by a multiple does not break the detailed balance condition, but the acceptance rate is improved. Therefore, it is sufficient to multiply both sides of the acceptance rate by a multiple and ensure that the two acceptance rates, after doubling, do not exceed 1. The general practice is to multiply the larger acceptance rate by 1. At this point, the most common MCMC method is obtained: the Metropolis-Hastings algorithm.

Gibbs Sampling

• The previous discussion mentioned that MCMC actually does not alter the transition probability matrix, thus requiring an acceptance rate supplement. Even after scaling, there is always an acceptance rate less than 1, which reduces the convergence efficiency. Gibbs sampling aims to find a transition matrix Q such that the acceptance rate equals 1.

• For the two-dimensional probability distribution \(p(x,y)\) , it is easy to obtain

  \[ \begin{aligned} p(x_1,y_1)p(y_2|x_1) & =p(x_1)p(y_1|x_1)p(y_2|x_1) \\ & =p(x_1)p(y_2|x_1)p(y_1|x_1) \\ & =p(x_1,y_2)p(y_1|x_1) \\ \end{aligned} \]

• From the left-hand side to the final form, this type is very similar to the detailed balance condition! In fact, if \(x=x_1\) is fixed, then \(p(y|x_1)\) can serve as the transition probability between any two different y-values on the line \(x=x_1\) . And this transition satisfies the detailed balance condition. Fixing y yields the same conclusion, therefore, between any two points in this two-dimensional plane, we can construct a transition probability matrix:

  • If two points are on the vertical line \(x=x_1\) , then \(Q=p(y|x_1)\)
  • If two points are on the horizontal line \(y=y_1\) , then \(Q=p(x|y_1)\)
  • If the line connecting two points is neither vertical nor horizontal, then applying the transition matrix Q to any two points on the plane in such a way satisfies the detailed balance condition; the Markov chain on this two-dimensional plane will converge to \(p(x,y)\) .

• After Gibbs sampling yields a new x dimension, the calculation of the new y dimension depends on the new x dimension because it is based on the previously selected coordinate axis transformation; otherwise, it cannot jump to the new state \((x_2,y_2)\) . What you actually get is \((x_1,y_2)\) and \((x_2,y_1)\) .

• Therefore, given a two-dimensional probability distribution, the transition probabilities along the horizontal or vertical directions satisfying the detailed balance condition on this plane can be calculated. Starting from any state on the plane, a single transition only changes the abscissa or ordinate, that is, it moves horizontally or vertically. From the formula of the detailed balance condition, it can be seen that this balance is transitive; if the transition in one dimension satisfies the balance condition and is followed by another dimension, then the equivalent single transition of the two transitions is also balanced.

• After all dimensions have been transferred once, a new sample is obtained. The sample sequence formed after the Markov chain converges is the random sample sequence we need. The state transition can be a cyclic transformation of the coordinate axes, i.e., this time horizontal transformation, next time vertical transformation, or it can be randomly selected each time. Although randomly selecting the coordinate axis each time will result in different new dimension values calculated in the middle, the stationary condition is not broken, and it can eventually converge to the same given distribution.

• Similarly, the aforementioned algorithm can be generalized to multi-dimensional spaces. When generalized to multi-dimensional spaces, the transition probability constructed on the \(x\) axis is \(Q=p(x|¬ x)\) . It is noteworthy that the sampling samples obtained from the above method are not mutually independent, but only conform to the given probability distribution.

Role in LDA

• Firstly, it is clear that the MCMC method is used to generate samples from a known distribution, but Gibbs sampling only requires the use of complete conditional probabilities, generating samples that satisfy the joint distribution, unlike general sampling methods that directly sample from the joint distribution
• Gibbs sampling has this characteristic that allows it to infer parameters without knowing the joint probability, and further derive the joint probability distribution
• However, in LDA, Gibbs sampling is not used to directly infer parameters, but rather to approximate the posterior, completing the step of updating the prior with data knowledge. Moreover, since LDA has the hidden variable of topics, the joint distribution of Gibbs sampling is not the topic distribution of documents or the word distribution of topics, and is not directly linked to the parameters of the LDA model. Gibbs sampling in LDA samples the topic assignment of tokens, i.e., the distribution of the hidden variables.
• However, after all token themes are assigned, the parameters of the LDA model are determined, and two multinomial distributions (parameters) can be obtained through classical probability (maximum likelihood estimation), and the corresponding Dirichlet distribution (posterior distribution of parameters) is also updated. Moreover, since the document-word matrix is decomposed into themes, in fact, we do not need to maintain the \(Document \* word\) matrix, but rather maintain the \(Document \* topic + topic \* word\) matrix.
• Gibbs sampling word topic assignment is actually calculating the posterior distribution of latent variables, thereby obtaining the posterior distribution of parameters.
• In Gibbs sampling, parameters are continuously updated, for instance, if the update in this iteration is \(p(x_1^{t+1})=p(x_1|x_2^t,x_3^t)\) , the next iteration becomes \(p(x_2^{t+1})=p(x_2|x_1^{t+1},x_3^t)\) , using the updated \(x_1^{t+1}\) for calculation. In LDA, this process is achieved by updating the topic of the sampled word. In Bayesian inference, data is divided into batches, and the posterior updates the prior in an iterative manner, which is further refined to each coordinate update in Gibbs sampling.
• The Gibbs sampling formula can be seen below, which can be interpreted as determining one's own theme distribution based on the thematic distribution of other words, and iteratively updating the thematic distribution of all words; how to determine it includes two parts, which are similar to the information provided by tf and idf.
• When calculating the posterior distribution of topic assignments based on the sampling formula, we do not directly obtain the posterior distribution of the parameters. However, after sampling new topics based on the posterior distribution of topic assignments and updating the statistics, since the Gibbs sampling formula itself includes the statistics, this is equivalent to completing the calculation of the posterior and updating the prior with a single step. Alternatively, it can also be understood that in LDA, we are always performing Bayesian inference on the distribution of topic assignments (latent variables), i.e., \(p(topic|word,doc)\) , and after completing this, performing a maximum likelihood estimation (classical type) based on the topic assignments allows us to obtain the parameters of the model.

Text Modeling

• Next, we discuss how to perform probabilistic modeling on text. The basic idea is that we assume all words in a document are generated according to a pre-set probability distribution, and we aim to find this probability distribution. Specifically, this is divided into the following two tasks:
  • What is the model like?
  • What is the generation probability of each word or the model parameters?

Unigram model

• What is the model like? The traditional unigram model, also known as the one-gram model, assumes that the generation of words is independent of each other; documents and words are independently exchangeable, regardless of order, as if all words are placed in a bag and a word is taken out each time according to a probability distribution, hence also known as the bag-of-words (BoW) model. The parameters of the bag-of-words model are the generation probabilities of each word, and the frequentist view holds that generation probabilities can be determined through word frequency statistics.

• Here introduces a Bayesian framework for unigrams, laying the groundwork for the derivation of the two-layer Bayesian framework for LDA in the following text. The Bayesian school believes that the generation of words is not only one layer: there are many kinds of probability distributions for word probabilities, and the probability distribution itself also follows a probability distribution, as if God has many dice, he picks one die and throws it again, generating a word.

• That is, the next document of the Unigram model is just a bag of words, with the generation of these words following a distribution, denoted as \(\mathop{p}^{\rightarrow}\) , and the distribution of word generation itself also follows a distribution, denoted as \(p(\mathop{p}^{\rightarrow})\) . Translated into mathematical formulas, the above two distributions represent the generation probability of a document:

  \[ p(W)=\int p(W|\mathop{p}^{\rightarrow})p(\mathop{p}^{\rightarrow})d\mathop{p}^{\rightarrow} \]

• In the view of the Bayesian school, we should first assume a prior distribution, and then correct it using training data. Here, we need to assume \(p(\mathop{p}^{\rightarrow})\) , which is the prior of the distribution, and what is the training data? It is the word frequency distribution extracted from the corpus. Assuming \(\mathop{n}^{\rightarrow}\) is the word frequency sequence of all words, then this sequence satisfies the multinomial distribution:

  \[ \begin{aligned} p(\mathop{n}^{\rightarrow}) &= Mult(\mathop{n}^{\rightarrow}|\mathop{p}^{\rightarrow},N) \\ &= C_N ^{\mathop{n}^{\rightarrow}} \prod_{k=1}^V p_k^{n_k} \\ \end{aligned} \]

• Since the training data satisfies multiple distributions, we naturally want to utilize the Dirichlet-Multinomial conjugacy, thus assuming the prior distribution of \(p(\mathop{p}^{\rightarrow})\) to be the Dirichlet distribution:

  \[ Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow})=\frac{1}{\int \prod_{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow}} \prod_{k=1}^V p_k^{\alpha _k -1} \]

  \(V\) is the size of the corpus dictionary, and the parameters \(\alpha\) of the Dirichlet distribution need to be set manually. After that, the posterior distribution of \(p(\mathop{p}^{\rightarrow})\) is obtained based on the conjugate after data correction:

  \[ \begin{aligned} p(\mathop{p}^{\rightarrow}|W,\mathop{\alpha}^{\rightarrow}) &= Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow})+MultCount(\mathop{n}^{\rightarrow}) \\ &= Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow}+\mathop{n}^{\rightarrow}) \\ \end{aligned} \]

• After obtaining the posterior, one can use maximum likelihood estimation or mean estimation to calculate \(\mathop{p}^{\rightarrow}\) , here we use the mean of the Dirichlet distribution from the posterior to estimate, combining the previously mentioned properties of the Dirichlet distribution, we have:

  \[ \mathop{p_i}^{~}=\frac{n_i+\alpha _i}{\sum _{i=1}^{V} (n_i+\alpha _i)} \]

  The physical interpretation of this formula: Unlike the general use of word frequency as an estimate, we first assume the word frequency (i.e., the prior pseudo-count \(\alpha _i\) ), then add the word frequency given by the data \(n_i\) , and normalize it as a probability.

• Now that the probability distribution of word generation \(\mathop{p}^{\rightarrow}\) has been obtained, the generation probability of documents under this distribution is obviously:

  \[ p(W|\mathop{p}^{\rightarrow})=\prod _{k=1}^V p_k^{n_k} \]

  The distribution of word generation probabilities, by bringing the conditional generation probability of documents under the word generation distribution into the previously mentioned document probability integral formula, yields the generation probability of the document under all distribution scenarios. Substituting and simplifying it results in a very nice formula.

  \[ p(W|\mathop{\alpha}^{\rightarrow})=\frac{\Delta(\mathop{\alpha}^{\rightarrow}+\mathop{n}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \]

  \(\Delta\) is the normalization factor:

  \[ \Delta(\mathop{\alpha}^{\rightarrow})=\int \prod _{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow} \]

PLSA model

• PLSA, or Probabilistic Latent Semantic Analysis model, posits that there exists an implicit thematic hierarchy between documents and words. Documents contain multiple themes, each corresponding to a distribution of words. When generating words, the model first selects a theme and then selects words from within that theme to generate them (in actual computation, it is the probability summation of each theme).
• Compared to the unigram model without Bayes, PLSA adds an additional layer of topics between documents and words.
• PLSA does not introduce Bayesian, it is just a model containing latent variables, performing maximum likelihood estimation, so the parameters can be iteratively learned using the EM algorithm, and the specific calculations are omitted here.

Role in LDA

• Now, let's organize, the Unigram model mainly includes two parts
  • Word Generation Probability Distribution
  • Parameter Distribution of Word Generation Probability Distribution
• PLSA model mainly consists of two parts
  • Word Generation Probability Distribution
  • Subject Generation Probability Distribution
• The Unigram model exhibits the distribution of the distribution, which is the significance of introducing parameter priors for the word distribution: making the word distribution a variable, turning the selection of a word from rolling a die into first selecting a die, and then rolling it to choose a word. Whether the introduction of priors is actually useful is a topic of contention between the Bayesian school and the frequentist school.
• PLSA model provides a very intuitive modeling for human language generation, introducing topics as implicit semantics, and defining the distribution of topic representative words, viewing articles as a mixture of topics.

LDA text modeling

Model Overview

• LDA integrates the advantages of Unigram and PLSA, adding Dirichlet prior assumptions for the word and topic dice respectively
  • Word Generation Probability Distribution (Temporarily Noted as A)
  • Parameter Distribution of Word Generation Probability Distribution (temporarily noted as B)
  • Subject Generation Probability Distribution (Temporarily Noted as C)
  • Parameter Distribution of the Probability Distribution of Topic Generation (temporarily denoted as D)
• It is easy for beginners to confuse that the topic generation probability distribution is not the parameter distribution of the word generation probability distribution; one must distinguish the hierarchical relationship in the LDA model from the conjugate relationships within each level. Additionally, the relationship between topics and words is not one-to-many; they are many-to-many. In fact, in the LDA model, a document is generated in this way (assuming there are K topics):
  • Sample K from the A distribution under the condition of the B distribution
  • For each document, a C distribution is obtained by drawing under the condition of the D distribution, and the following process is repeated to generate words:
    • From a C distribution, a topic z is sampled
    • From the z-th A distribution, a word is sampled
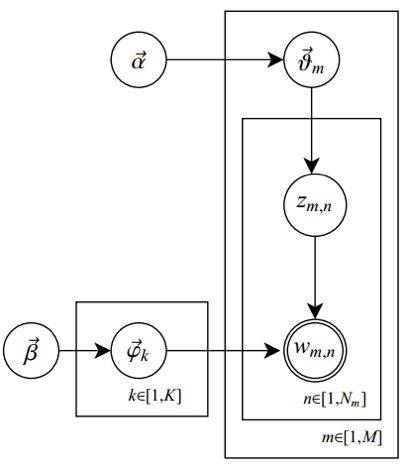
• Assuming there are \(m\) documents, \(n\) words, and \(k\) topics, then \(D+C\) is \(m\) independent Dirichlet-Multinomial conjugates, and \(B+A\) is \(k\) independent Dirichlet-Multinomial conjugates. The two Dirichlet parameters are a k-dimensional vector ( \(\alpha\) ) and an n-dimensional vector ( \(\beta\) ). Now we can understand the illustration at the beginning of this paper, where we express the symbols in their actual meanings, corresponding to the title illustration. This illustration actually describes these \(m+k\) independent Dirichlet-Multinomial conjugates in LDA:

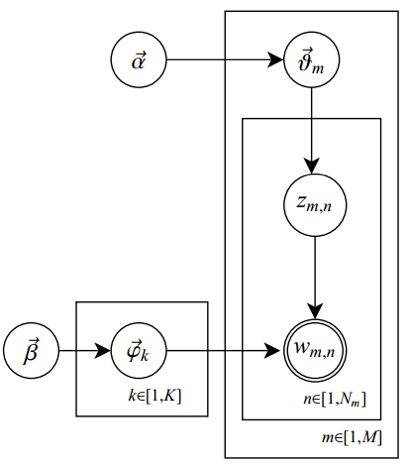
Establish distribution

• Now we can model the LDA topic model with \(m+k\) Dirichlet-Multinomial conjugate pairs, drawing on the final document generation distribution derived from the derivation of the Unigram model, we can separately calculate:

  \[ \begin{aligned} p(\mathop{z}^{\rightarrow}|\mathop{\alpha}^{\rightarrow}) = \prod _{m=1}^M \frac{\Delta(\mathop{n_m}^{\rightarrow}+\mathop{\alpha}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \\ p(\mathop{w}^{\rightarrow}|\mathop{z}^{\rightarrow},\mathop{\beta}^{\rightarrow}) = \prod _{k=1}^K \frac{\Delta(\mathop{n_k}^{\rightarrow}+\mathop{\beta}^{\rightarrow})}{\Delta(\mathop{\beta}^{\rightarrow})} \\ \end{aligned} \]

• The final result is the joint distribution of words and topics:

  \[ p(\mathop{w}^{\rightarrow},\mathop{z}^{\rightarrow}|\mathop{\alpha}^{\rightarrow},\mathop{\beta}^{\rightarrow}) = \prod _{m=1}^M \frac{\Delta(\mathop{n_m}^{\rightarrow}+\mathop{\alpha}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \prod _{k=1}^K \frac{\Delta(\mathop{n_k}^{\rightarrow}+\mathop{\beta}^{\rightarrow})}{\Delta(\mathop{\beta}^{\rightarrow})} \]

Sampling

• We mentioned earlier that we estimate model parameters within the framework of Bayesian inference, which requires us to obtain the posterior probability of topic assignments; here, Gibbs sampling is needed to help approximate the posterior

• According to the definition of Gibbs sampling, we need to sample using the fully conditional probability of topic assignments \(p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})\) , to approximate \(p(z_i=k|\mathop{w}^{\rightarrow})\) , \(z_i\) , which represent the topic of the ith word (here the subscript i represents the nth word in the mth document), while the vector w represents all the words we are currently observing.

• After establishing the entire probability model, we trained it using the following methods: we set the hyperparameters, randomly initialized various word frequency statistics (including the number of words of topic k in article m, the number of words of vocabulary t belonging to topic k, the total number of words in article m, and the total number of words in topic k), then sequentially performed Gibbs sampling on all words in the corpus, sampled their topics, and assigned this topic to the word, and updated the four word frequencies (i.e., using conjugate posterior updates), cyclically sampled until convergence, that is, the topic distribution after sampling basically conforms to the topic distribution generated by the model under the posterior probability, and the data can no longer provide more knowledge to the model (no longer updated).

  • Gibbs sampling requires restricting a certain dimension, sampling according to the conditional probability of the other dimensions, in text topic modeling, the dimension is the word, and calculating the conditional probability of the other dimensions is to exclude the count of the current word and its topic from the four word frequencies.
  • After sampling the topic, assign this topic to words, increase the frequency counts of four words, if it has converged, then the topic before and after sampling is the same, and if the word frequencies have not changed, it is equivalent to the posterior not being updated with knowledge from the data.

• Formula Derivation: The following section introduces two derivation methods, the first being the derivation based on the conjugate relationship as presented in the article "LDA Mathematical Mysteries," and the second being the derivation based on the joint distribution as described in the article "Parameter Estimation for Text Analysis."

• Based on the conjugation relationship, the following derivation is obtained:

• The object of the sample is the theme corresponding to the word, with a probability of:

  \[ p(z_i=k|\mathop{w}^{\rightarrow}) \]

• Using Gibbs sampling to sample the topic of a word requires calculating conditional probabilities with the topics of other words as conditions:

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow}) \]

• By Bayes' theorem, this conditional probability is proportional to (sampling, we can scale up the probabilities of each sample proportionally):

  \[ p(z_i=k,w_i=t|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow}) \]

• Expand this formula according to thematic distribution and word distribution:

  \[ \int p(z_i=k,w_i=t,\mathop{\vartheta _m}^{\rightarrow},\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\vartheta _m}^{\rightarrow} d\mathop{\varphi _k}^{\rightarrow} \]

• Since all the conjugates are independent, the above expression can be written as:

  \[ \int p(z_i=k,\mathop{\vartheta _m}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})p(w_i=t,\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\vartheta _m}^{\rightarrow} d\mathop{\varphi _k}^{\rightarrow} \]

• The probability chain is decomposed, and since the two expressions are respectively related to the topic distribution and the word distribution, they can be written as the product of two integrals:

  \[ \int p(z_i=k|\mathop{\vartheta _m}^{\rightarrow})p(\mathop{\vartheta _m}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\vartheta _m}^{\rightarrow} \cdot \int p(w_i=t|\mathop{\varphi _k}^{\rightarrow})p(\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\varphi _k}^{\rightarrow} \]

• Given the topic distribution of the mth document and the distribution of the kth topic word, we seek the probability of the ith word being t and the probability that the ith word corresponds to the kth topic, then it is obvious that:

  \[ p(z_i=k|\mathop{\vartheta _m}^{\rightarrow})=\mathop{\vartheta _{mk}} \\ p(w_i=t|\mathop{\varphi _k}^{\rightarrow})=\mathop{\varphi _{kt}} \\ \]

• And according to the conjugate relationship, there is

  \[ p(\mathop{\vartheta _m}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})=Dir(\mathop{\vartheta _m}^{\rightarrow}|\mathop{n_{m,¬ i}}^{\rightarrow}+\mathop{\alpha}^{\rightarrow}) \\ p(\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})=Dir(\mathop{\varphi _k}^{\rightarrow}|\mathop{n_{k,¬ i}}^{\rightarrow}+\mathop{\beta}^{\rightarrow}) \\ \]

• Therefore, the entire expression can be regarded as the product of the k-th and t-th terms of the expected vectors of two Dirichlet distributions. According to the properties of Dirichlet previously mentioned, it is easy to obtain that these expectations are fractional values obtained in proportion to the Dirichlet parameters, so the final probability calculation is (note that it is proportional to):

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})∝\frac{n_{m,¬ i}^{(k)}+\alpha _k}{\sum _{k=1}^K (n_{m,¬ i}^{(k)}+\alpha _k)} \cdot \frac{n_{k,¬ i}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k,¬ i}^{(t)}+\beta _t)} \]

• This probability can be understood as (excluding the current i-th token):

  \[ (文档m中主题k所占的比例) * (主题k中词t所占的比例） \]

• Observed that the denominator of the first term is the sum of the subject, which is actually unrelated to k, therefore it can be written as:

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})∝ (n_{m,¬ i}^{(k)}+\alpha _k) \cdot \frac{n_{k,¬ i}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k,¬ i}^{(t)}+\beta _t)} \]

• We take another look at how to derive based on the joint distribution

• We have previously obtained the joint distribution of words and topics:

  \[ p(\mathop{w}^{\rightarrow},\mathop{z}^{\rightarrow}|\mathop{\alpha}^{\rightarrow},\mathop{\beta}^{\rightarrow}) = \prod _{m=1}^M \frac{\Delta(\mathop{n_m}^{\rightarrow}+\mathop{\alpha}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \prod _{k=1}^K \frac{\Delta(\mathop{n_k}^{\rightarrow}+\mathop{\beta}^{\rightarrow})}{\Delta(\mathop{\beta}^{\rightarrow})} \]

• According to Bayes' formula, there is

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})=\frac{p(\mathop{w}^{\rightarrow},\mathop{z}^{\rightarrow})}{p(\mathop{w}^{\rightarrow},\mathop{z_{¬ i}}^{\rightarrow})} \\ =\frac{p(\mathop{w}^{\rightarrow}|\mathop{z}^{\rightarrow})} {p(\mathop{w_{¬ i}}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow})p(w_i)} \cdot \frac{p(\mathop{z}^{\rightarrow})} {\mathop{p(z_{¬ i})}^{\rightarrow}} \\ \]

• Since \(p(w_i)\) is an observable variable, we omit it, obtaining an expression proportional to it. We then express this expression in the form of \(\Delta\) (fraction divided by fraction, the denominators cancel each other out):

  \[ ∝ \frac{\Delta(\mathop{n_{z}}^{\rightarrow})+\mathop{\beta}^{\rightarrow}}{\Delta(\mathop{n_{z,¬ i}}^{\rightarrow})+\mathop{\beta}^{\rightarrow}} \cdot \frac{\Delta(\mathop{n_{m}}^{\rightarrow})+\mathop{\alpha}^{\rightarrow}}{\Delta(\mathop{n_{m,¬ i}}^{\rightarrow})+\mathop{\alpha}^{\rightarrow}} \]

• By substituting the expression of \(\Delta\) into the calculation, we can also obtain:

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})∝ (n_{m,¬ i}^{(k)}+\alpha _k) \cdot \frac{n_{k,¬ i}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k,¬ i}^{(t)}+\beta _t)} \]

• Text Analysis: A Pseudo-Algorithm Diagram of Gibbs Sampling for Parameter Estimation

i0oU6U.png

• It can be seen that the conditional probability is mainly calculated by recording four n values (two matrices and two vectors), and the topic is also updated by updating four n values for incremental updates. The algorithm first assigns initial values by random uniform sampling, and then updates the topic according to the sampling formula (first subtracting the old topic distribution and then adding the new topic distribution), where formula 78 is the \(p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})\) we calculated previously, and formulas 81 and 82 are the \(\mathop{\vartheta _{mk}},\mathop{\varphi _{kt}}\) . We can directly obtain them from the four n values, without considering the \(¬ i\) condition during sampling, specifically:

  \[ \mathop{\vartheta _{mk}} = \frac{n_{m}^{(k)}+\alpha _k}{\sum _{k=1}^K (n_{m}^{(t)}+\alpha _k)} \\ \mathop{\varphi _{kt}} = \frac{n_{k}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k}^{(t)}+\beta _t)} \]

Training and Testing

• Next, we train the LDA model, first randomly initializing the Dirichlet parameters (prior), then using text to supplement data knowledge, and finally obtaining the correct posterior. The training process is iterative:
  • Iterate what? Sample and update the themes corresponding to the words
  • What iteration? The complete conditional probability of Gibbs sampling
  • Iterative effects? Changes in topic allocation, changes in statistics, and changes in the fully conditional probability for the next Gibbs sampling
  • When to iterate? Gibbs sampling converges, i.e., the distribution of topics stabilizes and remains unchanged over a certain time interval, or the degree of model convergence is measured according to perplexity and other indicators.
• The difference between training and testing lies in that training involves sampling and updating the entire document collection, with both document-to-topic and topic-to-word distributions being updated, whereas testing retains the topic-to-word distribution unchanged, only sampling the current test document to convergence to obtain the topic distribution of that document.
• In fact, the two hyperparameters \(\alpha\) and \(\beta\) have undergone many iterations of posterior substitution for prior after training, with the parameter values becoming very large. \(\alpha\) discarded the final posterior result, and re-used the initial prior values when generating the topic distribution for new documents. This means that the document-to-topic distributions obtained during the training set are actually not usable when testing new documents. We utilize the topic-to-word distribution: because only the set of topics is for the entire document space (training set and test set), the topic-to-word distribution is also established on the dictionary of the entire document space. We retain the final posterior results for these k \(\beta\) vectors because this posterior has absorbed the likelihood knowledge of the data, resulting in large parameter values and small uncertainty. Essentially, each \(\beta\) vector is equivalent to determining a polynomial distribution from a topic to words, which is to say determining a topic. We use these determined topics to test the distribution of a new document across various topics. Therefore, when testing new documents, the parameter \(\alpha\) is generally set to be symmetric, i.e., with equal components (without prior preference for any particular topic), and with small values (i.e., high uncertainty; otherwise, the generated topic distribution would be uniform), which is analogous to the idea of maximum entropy. The test is conducted by using known fixed topics to obtain the document-to-topic distribution.
• LDA training is actually an unparameterized Bayesian inference, which can be implemented using MCMC and non-MCMC methods. Among the MCMC methods, Gibbs sampling is often used, while non-MCMC methods can employ variational inference and other iterative approaches to obtain parameters.

LDA in Gensim

• Gensim's LDA provides several parameters, among which the default value for \(\alpha\) is as follows:

  alpha ({numpy.ndarray, str}, optional) – Can be set to an 1D array of length equal to the number of expected topics that expresses our a-priori belief for the each topics’ probability. Alternatively, default prior selecting strategies can be employed by supplying a string: 'asymmetric': Uses a fixed normalized asymmetric prior of 1.0 / topicno. 'default': Learns an asymmetric prior from the corpus.

  Gensimmodels.ldamodel – Latent Dirichlet Allocation

• gensim does not expose \(\beta\) to users; users can only set \(\alpha\) , which can be customized and can also be set as symmetric or asymmetric. The symmetric setting means all are 1, while the asymmetric setting fits the Zipf law (?), and it is possible that \(\beta\) has an asymmetric default setting.

More

• Parameter estimation for text analysis points out that hidden topics actually come from high-order co-occurrence relationships between words

• LDA is used for document query, where LDA is trained on candidates, and a test is conducted each time a new query is received

  • Based on a similarity ranking method, the similarity between the topic distribution of candidates and queries is calculated using JS distance or KL divergence, and then sorted

  • Based on the Predictive likelihood ranking method, calculate the probability of each candidate appearing for a given query, based on thematic decomposition of topic z:

    \[ \begin{aligned} p\left(\vec{w}_{m} | \tilde{\vec{w}}_{\tilde{m}}\right) &=\sum_{k=1}^{K} p\left(\vec{w}_{m} | z=k\right) p\left(z=k | \tilde{\vec{w}}_{\tilde{m}}\right) \\ &=\sum_{k=1}^{K} \frac{p\left(z=k | \vec{w}_{m}\right) p\left(\vec{w}_{m}\right)}{p(z=k)} p\left(z=k | \tilde{\vec{w}}_{\tilde{m}}\right) \\ &=\sum_{k=1}^{K} \vartheta_{m, k} \frac{n_{m}}{n_{k}} \vartheta_{\tilde{m}, k} \end{aligned} \]

• LDA for clustering

  • In fact, the distribution of topics is a soft clustering division of documents. If each document is assigned to the topic with the highest probability, that would be a hard division.
  • Or use topic distribution as the feature vector of the document and then further cluster using various clustering algorithms
  • Evaluation of clustering results can utilize a known clustering partitioning result as a reference, and assess using the Variation of Information distance

• LDA evaluation metrics, perplexity, defined as the reciprocal geometric mean of the likelihood measured on the validation set:

  \[ \mathrm{P}(\tilde{\boldsymbol{W}} | \boldsymbol{M})=\prod_{m=1}^{M} p\left(\tilde{\vec{w}}_{\tilde{m}} | \mathcal{M}\right)^{-\frac{1}{N}}=\exp -\frac{\sum_{m=1}^{M} \log p\left(\tilde{\bar{w}}_{\tilde{m}} | \mathcal{M}\right)}{\sum_{m=1}^{M} N_{m}} \]

• Assuming the distribution of the validation set and the training set is consistent, a high perplexity of LDA on the validation set indicates a larger entropy, greater uncertainty, and that the model has not yet learned a stable parameter.

LDA用来做什么

• LDA是一种主题模型，问题实际上是主题模型是用来做什么？用来表示文档 。在这里将文档看成一个词袋。
• 如果将词典里每一个词看成一个特征，tfidf值作为特征值大小来表示文档，则文档的特征向量太过稀疏，且维度太高
• LSI的解决办法是，将文档-词的矩阵进行奇异值分解，降维，但是这样得到的降维空间，即词到文档之间的隐变量无法解释，纯数学的方法，太暴力
• PLSA提出了隐变量应该是主题，可以把文档表示为主题向量，而主题定义为在词典上的某一种多项式分布，这样PLSA中包含了两层多项式分布：文档到主题的多项式分布（文档中各个主题的混合比例，即文档的特征向量），主题到词的多项式分布（在整个词典上的概率分布，表示不同主题下各个词出现的概率）
• LDA则对这两个多项式分布的参数制定了迪利克雷先验，为PLSA引入贝叶斯框架

贝叶斯模型

• LDA是一种贝叶斯模型

• 给定训练数据，贝叶斯模型怎么学习参数(参数的分布）：贝叶斯估计

  • 先给参数一个先验分布\(p(\theta)\)

  • 给定数据，计算似然\(p(X|\theta)\)和evidence\(P(X)\)，根据贝叶斯公式计算参数的后验分布

  • 后验分布就是学习到的参数分布

    \[ p(\vartheta | X)=\frac{p(X | \vartheta) \cdot p(\vartheta)}{p(\mathcal{X})} \]

• 可能数据太多，那就分批更新，上一次更新后得到的后验作为下一次更新的先验，类似于随机梯度下降中的思想

• 对于新数据的似然，不像最大似然估计或者最大后验估计，两者是点估计，直接算\(p(x_{new}|\theta _{ML})\),\(p(x_{new}|\theta _{MAP})\)，贝叶斯估计需要对参数分布求积分：

  \[ \begin{aligned} p(\tilde{x} | X) &=\int_{\vartheta \in \Theta} p(\tilde{x} | \vartheta) p(\vartheta | X) \mathrm{d} \vartheta \\ &=\int_{\vartheta \in \Theta} p(\tilde{x} | \vartheta) \frac{p(X | \vartheta) p(\vartheta)}{p(X)} \mathrm{d} \vartheta \end{aligned} \]

• 贝叶斯估计里常常出现两个问题

  • 有了先验，有了似然，计算出的后验很复杂
  • evidence很难算

• 因此共轭和gibbs sampling分别解决这两个问题

  • 共轭：给定似然，找一个先验，使得后验的形式和先验一致
  • gibbs sampling：利用MCMC的思路去近似后验，而不用显式的计算evidence

• 假如是带隐变量的贝叶斯模型，那么有

  \[ p(\vartheta|x) = \int_{z} p(\vartheta|z)p(z|x) \]

• 在LDA当中，隐变量z就是词所属的主题（词的主题分配），那么\(p(\vartheta|z)\)自然是很好求的，那么剩下的\(p(z|x)\)，就再套上面贝叶斯推断的公式:

  \[ p(z | X)=\frac{p(X | z) \cdot p(z)}{p(\mathcal{X})} \]

• 在介绍LDA之前，介绍了其他两个模型，带贝叶斯的unigram以及plsa，前者可以看成是没有主题层的LDA，后者可以看成是没有贝叶斯的LDA

• 接下来就分别介绍共轭、gibbs sampling、带贝叶斯的unigram/plsa，最后介绍LDA

共轭

Gamma函数

• 定义

  \[ \Gamma (x) = \int _0 ^{\infty} t^{x-1} e^{-t} dt \]

• 因为其递归性质\(\Gamma(x+1)=x\Gamma(x)\)，可以将阶乘的定义扩展到实数域，进而将函数导数的定义扩展到实数集，例如计算1/2阶导数

• Bohr-Mullerup定理：如果\(f:(0,\infty) \rightarrow (0,\infty)\)，且满足

  • \(f(1)=1\)
  • \(f(x+1)=xf(x)\)
  • \(log f(x)\)是凸函数 那么\(f(x)=\Gamma(x)\)

• Digamma函数

  \[ \psi (x)=\frac{d log \Gamma(x)}{dx} \]

  其具有以下性质

  \[ \psi (x+1)=\psi (x)+\frac 1x \]

• 在用变分推断对LDA进行推断时结果就是digamma函数的形式

Gamma分布

• 将上式变换

  \[ \int _0 ^{\infty} \frac{x^{\alpha -1}e^{-x}}{\Gamma(\alpha)}dx = 1 \]

  因此可取积分中的函数作为概率密度，得到形式最简单的Gamma分布的密度函数：

  \[ Gamma_{\alpha}(x)=\frac{x^{\alpha -1}e^{-x}}{\Gamma(\alpha)} \]

• 指数分布和\(\chi ^2\)分布都是特殊的Gamma分布，且作为先验分布非常有用，广泛应用于贝叶斯分析当中。

• Gamma分布与泊松分布具有形式上的一致性，实际上在两者的通常表示中，仅仅只有参数差1的区别，且之前说到阶乘可以用Gamma函数表示，因此可以直观的认为Gamma分布是Poisson分布在正实数集上的连续化版本。

  \[ Poisson(X=k|\lambda)=\frac{\lambda ^k e^{-\lambda}}{k!} \]

• 令二项分布中\(np=\lambda\)，当n趋向于无穷且p趋向于0时，泊松分布就是二项分布的极限分布。经常用于解释泊松分布的一个例子是交换机接收呼叫，假设将整个时间分成若干个时间段，每个时间段内至多达到一次呼叫，概率为p，则总体呼叫数符合一个二项分布，当np为定值\(\lambda\)时，将时间分为无穷个段，几乎是连续的，取\(p=\frac{\lambda}{n}\)带入二项分布，取极限后即得到泊松分布。在此基础上分布的取值连续化（即将泊松分布中k的阶乘用Gamma函数替代）就得到Gamma分布。

Beta分布

• 背景：

  • 现在有n个在[0,1]区间上均匀分布的随机变量，将这n个随机变量按大小排序后，如何求得第k个顺序统计量\(p=x_k\)的分布？

  • 为了求分布，利用极限的思想，我们求这个变量落在一小段区间上的概率\(x \leq X_{k} \leq x+\Delta x\)

  • 将整个区间分为三部分：小区间以前，小区间，小区间以后，若小区间内只有第k大的数，则小区间以前应该有k-1个数，小区间以后应该有n-k个数,这种情况的概率为

    \[ \begin{aligned} P(E)&=x^{k-1}(1-x-\Delta x)^{n-k}\Delta x \\ &=x^{k-1}(1-x)^{n-k}\Delta x+\omicron (\Delta x) \\ \end{aligned} \]

  • 若小区间内有两个及两个以上的数，计算可得这种情况的概率是\(\omicron (\Delta x)\)，因此只考虑小区间内只有第k大的数，此时令\(\Delta x\)趋向于0，则得到第k大数的概率密度函数（注意事件E的系数应该是\(nC_n^k\)）：

    \[ f(x)=\frac{n!}{(k-1)!(n-k)!}x^{k-1}(1-x)^{n-k} \quad x \in [0,1] \]

    用Gamma函数表示（令\(\alpha =k,\beta = n-k+1\)）得到:

    \[ \begin{aligned} f(x)&=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1} \\ &=Beta(p|k,n-k+1) \\ &=Beta(\alpha,\beta) \\ \end{aligned} \]

    这就是Beta分布，我们可以取概率分布最大的点作为第k大数的预测值。

• Beta分布实际上是对分布的预测，即分布的分布。在背景里，我们要找第k大顺序统计量的概率分布，我们把这个第k大顺序统计量记作p，现在知道有n个在[0,1]区间上均匀分布的值，n和k建立了一个在[0,1]区间内的相对位置，这也就是\(\alpha\)和\(\beta\)的作用（因为\(\alpha\)和\(\beta\)就是n和k计算出来的），代表我倾向于认为p在[0,1]中的哪里。因为n个统计量是均匀分布的，而p是其中第k大的，那么p就倾向于在\(\frac kn\)这个位置。
• 因此Beta分布的参数（\(\alpha\)和\(\beta\)）意义很明显了，就是我在什么都不知道的情况下，先入为主的认为p可能所在的位置，即先验，而Beta分布的结果就是在这种先验影响下，计算出来的p的分布，这个p的实际含义，是二项式分布的参数。因此，Beta分布可以作为二项式分布的参数先验。

Beta-Binomial共轭

• 这样我们可以对第k大数的分布建立一个Beta分布的先验，如果现在我们知道有m个在[0,1]之间均匀分布的数，且其中有几个比第k大数大，有几个比第k大数小，则可以将其作为一种数据知识补充进去，形成后验分布。
• 假设要猜的数\(p=X_k\)，现在我们知道了有\(m_1\)个数比\(p\)小，\(m_2\)个数比\(p\)大，显然此时\(p\)的概率密度函数就变成了\(Beta(p|k+m_1,n-k+1+m_2)\)
• 补充进m个数的数据知识相对于做了m次贝努利实验，因为我们讨论的范围在[0,1]上，m个数只关心比\(p\)大还是小，\(p=X_k\)的数值便可以代表这一概率，因此\(m_1\)服从二项分布\(B(m,p)\)

先验	数据知识	后验
Beta分布	二项分布	Beta分布

• 因此我们可以得到Beta-Binomial共轭

  \[ Beta(p|\alpha,\beta)+BinomCount(m_1,m_2)=Beta(p|\alpha+m_1,\beta+m_2) \]

  即数据符合二项分布时，参数的先验分布和后验分布都能保持Beta分布的形式，我们能够在先验分布中赋予参数明确的物理意义，并将其延续到后验分布中进行解释，因此一般将Beta分布中的参数\(\alpha,\beta\)称为伪计数，表示物理计数。

• 可以验证的是当Beta分布的两个参数均为1时，就是均匀分布，这时对共轭关系可以看成：开始对硬币不均匀性不知道，假设硬币正面向上的概率为均匀分布，在投掷了m次硬币后，获得了\(m_1\)次向上其他次向下的数据知识，通过贝叶斯公式计算后验概率，可以算出正面向上的概率正好是\(Beta(p|m_1+1,m_2+1)\)

• 通过这个共轭，我们可以推出关于二项分布的一个重要公式：

  \[ P(C \leq k) = \frac{n!}{k!(n-k-1)!}\int _p ^1 t^k(1-t)^{n-k-1}dt \quad C \sim B(n,p) \]

  现在可以证明如下：

  • 式子左边是二项分布的概率累积，式子右边时是\(Beta(t|k+1,n-k)\)分布的概率积分

  • 取n个随机变量，均匀分布于[0,1]，对于二项分布\(B(n,p)\)，若数小于\(p\)则是成功，否则失败，则n个随机变量小于\(p\)的个数C符合二项分布\(B(n,p)\)

  • 此时可以得到\(P(C \leq k)=P(X_{k+1}>p)\)，即n个随机变量按顺序排好后，小于\(p\)的有\(k\)个

  • 这时利用我们对第k大数的概率密度计算出为Beta分布，带入有

    \[ \begin{aligned} P(C \leq k) &=P(X_{k+1} > p) \\ &=\int _p ^1 Beta(t|k+1,n-k)dt \\ &=\frac{n!}{k!(n-k-1)!}\int _p ^1 t^k(1-t)^{n-k-1}dt \\ \end{aligned} \]

    即证

• 通过这个式子，将n取极限到无穷大，转换为泊松分布，可以推导出Gamma分布。

• 在本节中，我们为先验引入了其他信息，就是有几个数比第k大数大和小，这些信息相当于是告诉我：我可以修改p的先验，我之前倾向于认为的p的位置改动了。假如我知道了几个数比p大，那么p的先验位置应该往后移，如果我知道了几个数比p小，那么p的先验位置应该往前移，如果我同时知道了100个数比p大，100个数比p小呢？p的位置不变，但是我更加确信了p真实的位置就是现在这个先验位置，因此Beta分布在这个先验位置上更集中，从后文分析Dirichlet参数的意义中我们会再次看到这一点。先验加上数据知识修改之后，就形成了后验，这就是贝叶斯公式的基本内容。

Dirichlet-Multinomial共轭

• 假设我们不仅要猜一个数，还要猜两个数\(x_{k_1},x_{k_1+k_2}\)的联合分布，该如何计算？

• 同理，我们设置两个极小区间\(\Delta x\)，将整个区间分为五块，极小区间之间分别为\(x_1,x_2,x_3\)计算之后可以得到

  \[ f(x_1,x_2,x_3)=\frac{\Gamma(n+1)}{\Gamma(k_1)\Gamma(k_2)\Gamma(n-k_1-k_2+1)}x_1^{k_1-1}x_2^{k_2-1}x_3^{n-k_1-k_2} \]

• 整理一下可以写成

  \[ f(x_1,x_2,x_3)=\frac{\Gamma(\alpha _1+\alpha _2+\alpha _3)}{\Gamma(\alpha _1)\Gamma(\alpha _2)\Gamma(\alpha _3)}x_1^{\alpha _1-1}x_2^{\alpha _2-1}x_3^{\alpha _3-1} \]

  这就是3维形式的Dirichlet分布。其中\(x_1,x_2,x_3\)（实际上只有两个变量）确定了两个顺序数联合分布，\(f\)代表概率密度。

• 注意到在\(\alpha\)确定的情况下，前面的一堆gamma函数其实是概率归一化的分母，后文我们将Dirichlet分布更一般的写成：

  \[ Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow})=\frac{1}{\int \prod_{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow}} \prod_{k=1}^V p_k^{\alpha _k -1} \]

• 其中归一化分母，也即那一堆gamma，令其为：

  \[ \Delta(\mathop{\alpha}^{\rightarrow})=\int \prod _{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow} \]

• 同样，我们也可以对Dirichlet分布的先验加入数据知识，其后验依然是Dirichlet分布

  \[ Dir(p|\alpha)+MultCount(m)=Dir(p|\alpha+m) \]

  上式中的参数均是向量，对应多维情况。

• 无论是Beta分布还是Dirichlet分布，都有一个很重要的性质，即他们的均值可以用参数的比例表示，例如对于Beta分布，\(E(p)=\frac{\alpha}{\alpha+\beta}\)，对于Dirichlet分布，均值是一个向量，对应于各个参数比例组成的向量。

Dirichlet分析

• 根据Dirichlet的性质，其参数比例代表了[0,1]上的一个划分，决定了dirichlet分布高概率的位置，其参数大小决定了高概率的比例（陡峭），例如下图，多项式分布有三项，参数分别为\(p_1,p_2,p_3\)，他们的和为一且各项大于零，在三维空间内便是一个三角面，面上每一点代表一种多项式分布，红色区域概率高，蓝色区域概率低：

i0orkR.png

• \(\alpha\)控制了多项式分布参数的mean shape和sparsity。
• 最左边，Dirichlet的三个参数\(\alpha _1,\alpha _2,\alpha _3\)相等，代表其红色区域位置居中，且三个\(\alpha\)的值均较大，红色区域较小，把热力图看成等高线图的话就代表红色区域较陡峭，说明Dirichlet非常确认多项式分布的参数会在居中的位置。对于三个多项式分布的参数\(p_1,p_2,p_3\)来说，较大可能取到三个p等值的情况。
• 中间的图，三个\(\alpha\)不相等，某一个\(\alpha\)偏大，导致红色区域偏向三角面某一角，导致某一个p取值较大，其余两个p取值较小的可能性比较大，这时体现参数先验的参数作为concentration的作用，将概率注意力集中于某些项。
• 最右边，同最左边，三个\(\alpha\)相等，红色区域居中，但是\(\alpha\)的值均偏小，导致红色区域发散，也就是Dirichlet认为三个p的值应该在最中间，但是不那么确定。结果就是三个p之间有差别，但差别不会太大（依然在最中间附近），不会出现非常陡峭的情况（最陡峭也就是最中间无限高，概率为1，三个p值一定相同）
• 因此可以看出，\(\alpha\)的比例决定了多项式分布高概率的位置，也就是主要确定了各个\(p\)的比例，定好concentration，而\(\alpha\)的大小决定了这个位置的集中情况，\(\alpha\)越小，位置越集中，p的分布越确定，反之p的分布由红色区域位置大致确定，但是变化范围较大。
• 当\(\alpha\)远小于1时，Dirichelt分布会走向另一个极端，在上面这个三角面的例子里，红色区域依然会陡峭，但是陡峭在三角面的三个角上，可以想成\(alpha\)从大变到1，再变小，大概率密度区域从最中间慢慢分散到整个面，然后又聚集在三个角。
• 再来看看维基百科中关于Dirichlet参数\(\alpha\)的描述：

  The concentration parameter Dirichlet distributions are very often used as prior distributions in Bayesian inference. The simplest and perhaps most common type of Dirichlet prior is the symmetric Dirichlet distribution, where all parameters are equal. This corresponds to the case where you have no prior information to favor one component over any other. As described above, the single value α to which all parameters are set is called the concentration parameter. If the sample space of the Dirichlet distribution is interpreted as a discrete probability distribution, then intuitively the concentration parameter can be thought of as determining how "concentrated" the probability mass of a sample from a Dirichlet distribution is likely to be. With a value much less than 1, the mass will be highly concentrated in a few components, and all the rest will have almost no mass. With a value much greater than 1, the mass will be dispersed almost equally among all the components. See the article on the concentration parameter for further discussion.

  Dirichlet_distributionIntuitive interpretations of the parameters

• 当\(\alpha\)远小于1时，概率密度会主要堆积在一个或少数几个项上，也就是红色区域聚集在三个角的情况，这时Dirichlet分布抽样得到的多项式分布大概率在角上，也就是概率密度堆积在一个项上，其余两个项概率近似为0。\(\alpha\)远大于1时，概率密度会分散到各个部分，就是对应三图中最左边的图，三个项概率相差不大的可能性比较大。

Role in LDA

• 总结一下共轭：设有分布A，A的参数分布（或者叫分布的分布）为B，若B的先验在获得A的数据知识之后得到的后验与先验属于同一类分布，则A与B共轭，B称为A的参数共轭分布（或者叫先验共轭） ，在上文提到的例子里，Beta分布是二项分布的参数共轭分布，Dirichlet分布是多项式分布的参数共轭分布。
• LDA实际上是将文本生成建模为一个概率生成模型，具体而言是一个三层贝叶斯模型，并且针对文档-主题和主题-词语两个multinomial分布都假设其参数先验为Dirichlet分布，用Dirichlet-Multinomial共轭来利用数据知识更新其后验。
• 为了介绍Dirichlet-Multinomial共轭，先介绍Gamma函数及其分布，Gamma函数将阶乘扩展到实数域，之后介绍了能估计分布的Beta函数，在引入了Gamma函数之后Beta分布的参数能扩展到实数域。之后介绍了Beta-Binomial共轭，这种共轭带来的好处是在用数据训练修正时，我们已经知道了后验分布的形式，之后将这种共轭关系扩展到高维（估计多个分布），就得到了Dirichlet-Multinomial共轭。
• 为文档到主题和主题到词的两个多项式分布加入Dirichlet分布作为参数先验的好处是：将多项式参数作为变量，先验信息指导了参数在哪个范围内变动，而不是具体的值，使得模型在小训练样本内的泛化能力更强。
• 在Dirichlet Process中\(\alpha\)的大小体现了Dirichlet分布拟合Base Measure时的离散程度，\(\alpha\)越大，越不离散，各个项均能得到差不多的概率。
• 对应到LDA模型中，这种离散程度就代表了文档是集中在某几个主题上还是在所有主题上较均匀的分布，或者主题是集中在少数词上还是在整体的词上较均匀的分布。

吉步斯采样

随机模拟

• 即蒙特卡洛的含义，用于已知分布，需要生成一系列满足此分布的随机样本，并用这些样本的统计量来估计原分布一些不好直接解析计算的参数。
• 马尔可夫是指产生随机样本的方法依赖于马氏链的性质，通过构造马氏链当中的转移矩阵，使得马氏链收敛时能够产生满足给定分布的样本序列。
• MCMC的一种方法是随机采样，利用已知分布计算出接受率，只接收部分采样，而吉布斯采样是接受率为1的一种MCMC方法。它提升了接受率，但是加长了采样过程。

马氏链

• 马氏链即状态转移的概率只依赖于前一个状态
• 因为转移概率只依赖于前一个状态，因此可以将状态转移概率写成转移概率矩阵，经过n次转移之后的各状态概率分布即初始状态概率分布向量乘以矩阵的n次幂得到的结果
• 矩阵的幂从某一次数之后不变，即每一行收敛成相同的概率分布，同时初始概率转移足够多次之后也收敛成相同的分布
• 关于马氏链收敛的定义
  • 如果一个非周期马氏链具有转移概率矩阵P（可以有无穷多状态），且它的两个任何状态是联通（任何两个状态可以通过有限步转移到达）的，则\(lim_{n \rightarrow \infty}P_{ij}^n\)存在且与\(i\)无关，记这个收敛的矩阵为\(\pi(j)\)
  • \(\pi (j)=\sum _{i=0}^{\infty} \pi (i) P_{ij}\)
  • \(\pi\)是方程$P = $的唯一非负解
  • \(\pi\)称为马氏链的平稳分布

Markov Chain Monte Carlo

• 回到随机生成，对于给定的概率分布，我们希望能生成它对应的样本，一个想法就是构造一个马氏链，其平稳分布刚好就是这个概率分布：因为当马氏链收敛以后，其平稳分布就是各个状态的概率分布，收敛后无论经过状态转移生成多长的状态序列，这个序列里状态的分布一直保持着平稳分布。若平稳分布是要生成的概率分布，则状态序列就是给定概率分布下的一个随机样本序列。

• 因此，问题在于，如何已知平稳分布构造马氏链的状态转移矩阵。主要利用了非周期马氏链的细致平稳条件：若\(\pi(i)P_{ij}=\pi(j)P_{ij} \quad for \quad all \quad i,j\)，则\(\pi(x)\)是马氏链的平稳分布。这个定理一个物理解释是：若状态i的概率质量是稳定的，则从状态i转移到状态j变化的概率质量恰好和从状态j转移到状态i变化的概率质量互补。

• 设从状态i转移到状态j的概率为\(q(i,j)\)，若\(p(i)q(i,j)=p(j)q(j,i)\)，那么此时\(p(x)\)就是这个马氏链的平稳分布，转移矩阵也不用改了，但一般情况下你的运气没有那么好，在已知\(p(x)\)的情况下，我们需要对\(q\)进行改造，为此我们乘上一个接受率\(\alpha\)，使得：

  \[ p(i)q(i,j)\alpha (i,j)=p(j)q(j,i)\alpha (j,i) \]

  为什么叫接受率？因为可以理解为这个\(\alpha\)是在原来的状态转移之后再乘一个概率，代表是否接受这次转移。

• 如何确定接受率？其实显而易见\(\alpha (i,j)=p(j)q(j,i)\)，对称构造即可。

• 因此在每次转移之后，我们从均匀分布采样一个变量，若变量小于接受率则按原始状态转移矩阵进行转移，否则不转移。

• 这样的MCMC采样算法存在一个问题，我们其实没有改动原始状态转移矩阵q，而是根据q计算了接受率来保证收敛到p，但是接受率可能计算出来很小，导致状态长期原地踏步，收敛缓慢。事实上，将式\(p(i)q(i,j)\alpha (i,j)=p(j)q(j,i)\alpha(j,i)\)两边同时乘以一个倍数，细致平稳条件没有被打破，但是接受率获得了提高，因此只要将两边接受率乘以一个倍数并保证两个接受率翻倍之后不大于1即可，一般做法是将较大的接受率乘到1。这时就得到了最常见的一种MCMC方法：Metropolis-Hastings算法。

Gibbs Sampling

• 之前说到了MCMC实际上没有对状态转移矩阵改动，因此需要一个接受率补充，即便放缩之后总有一个接受率小于1，降低了收敛效率。吉步斯采样希望找到一个转移矩阵Q使得接受率等于1。

• 对二维概率分布\(p(x,y)\)，易得到

  \[ \begin{aligned} p(x_1,y_1)p(y_2|x_1) & =p(x_1)p(y_1|x_1)p(y_2|x_1) \\ & =p(x_1)p(y_2|x_1)p(y_1|x_1) \\ & =p(x_1,y_2)p(y_1|x_1) \\ \end{aligned} \]

• 从左式到最终式，这种形式非常像细致平稳条件！实际上假如固定\(x=x_1\)，则\(p(y|x_1)\)可以作为直线\(x=x_1\)上任意两个不同y值的点之间的转移概率，且这种转移满足细致平稳条件。固定y我们能得到相同的结论，因此在这个二位平面上任意两点之间我们可以构造转移概率矩阵：

  • 若两点在垂直线\(x=x_1\)上，则\(Q=p(y|x_1)\)
  • 若两点在水平线\(y=y_1\)上，则\(Q=p(x|y_1)\)
  • 若两点连线既不垂直也水平，则\(Q=0\) 这样对平面上任意两点应用转移矩阵Q，均满足细致平稳条件，这个二维平面上的马氏链将收敛到\(p(x,y)\)。

• gibbs采样得到新的x维度之后，在计算新的y维度时是依赖了新的x维度，因为是在之前选定坐标轴转换的基础上再进行转移，不然无法跳转到新状态\((x_2,y_2)\)，你得到的实际上是\((x_1,y_2)\)和\((x_2,y_1)\)。

• 因此，给定二维概率分布，可以计算出这个平面上沿水平或者垂直方向的满足细致平稳条件的转移概率，从平面上任何一点状态出发，它一次转移只改变横坐标或者纵坐标，也就是水平或者垂直移动，从细致平稳条件的公式可以看到这个平稳是可以传递的，如果从某一个维度的转移满足平稳条件，之后接着另一个维度，那么两次转移所等效的一次转移也是平稳的。

• 等到所有维度都转移了一次，就得到了一个新的样本。等到马氏链收敛之后形成的样本序列就是我们所需要的随机生成样本序列。状态的转移可以是坐标轴轮流变换的，即这次水平转换，下次垂直转换，也可以每次随机选择坐标轴。虽然每次随机选择坐标轴会导致中途计算出来的新的维度值不一样，但是平稳条件没有打破，最终能够收敛到一样的给定分布。

• 同样，上述算法也可以推广到多维。扩展到多维时，在\(x\)轴上构建的的转移概率就是\(Q=p(x|¬ x)\)。值得注意的是，上述得到的采样样本并不是相互独立的，只是符合给定的概率分布。

Role in LDA

• 首先明确，MCMC方法是产生已知分布的样本，但是gibbs采样只需要使用完全条件概率，产生了满足联合分布的样本，而不像一般采样方法直接从联合分布中采样
• gibbs采样这种特性就使其可以在不知道联合概率的情况下去推断参数，进一步推出联合概率分布
• 但是在LDA中，并没有用gibbs sampling去直接推断参数，而是用其去近似后验，完成用数据知识更新先验这一步。而且由于LDA存在着主题这一隐变量，gibbs采样的联合分布并不是文档的主题分布或者主题的词分布，和LDA模型的参数没有直接挂钩。Gibbs sampling在LDA中采样的是token的主题分配，即隐变量的分布。
• 但是所有token主题分配确定之后，LDA模型的参数就确定了，通过古典概型（最大似然估计）就可以得到两个multinomial分布（参数），对应的dirichelt分布（参数后验分布）也得到更新。且由于引入了主题分解了文档-单词矩阵，实际上我们不需要维护\(Document \* word\)矩阵，而是维护\(Document \* topic + topic \* word\)即可。
• gibbs采样词的主题分配，实际上是在计算隐变量分布的后验，进而得到参数分布的后验。
• gibbs采样中在不断更新参数，例如本次迭代更新\(p(x_1^{t+1})=p(x_1|x_2^t,x_3^t)\)，则下一次迭代为\(p(x_2^{t+1})=p(x_2|x_1^{t+1},x_3^t)\)，即使用更新之后的\(x_1^{t+1}\)来计算。在LDA中，这一过程通过更新被采样单词的主题实现。贝叶斯推断中将数据分批，用后验更新先验的迭代，在这里被进一步细化到了gibbs sampling的每一次坐标更新。
• 下文可以看到gibbs采样公式，可以解释为根据其他词的主题分配情况决定自己的主题分配，迭代更新所有词的主题分配；具体如何决定，包含了两个部分，这两个部分类似于tf和idf提供的信息。
• 当根据采样公式计算出主题分配的后验时，我们并没有直接得到参数的后验分布，但是当根据主题分配后验采样出新主题，更新了统计量之后，由于gibbs sampling公式里本身包含了统计量，这里相当于计算后验和用后验更新先验一步完成。或者也可以理解成，LDA里一直做的是主题分配分布（隐变量）的贝叶斯推断，即\(p(topic|word,doc)\)，做完之后根据主题分配，做一次最大似然估计（古典概型）就能得到模型的参数。

文本建模

• 接下来讨论如何对文本进行概率建模，基本思想是我们假设一个文档中所有的词是按照一种预先设置的概率分布生成的，我们希望找到这个概率分布。具体而言分为以下两个任务：
  • 模型是怎样的？
  • 各个词的生成概率或者说模型参数是多少？

Unigram模型

• 模型是怎样的？传统的unigram模型即一元语法模型，认为各个词之间的生成是独立的，文档之间、词之间都是独立可交换的，无所谓顺序，就像所有的词放在一个袋子里，每次按概率分布取出一个词，因此也叫词袋模型(BoW)。词袋模型的参数就是各个词的生成概率，频率派认为可以通过词频统计确定生成概率。

• 这里为unigram引入一层贝叶斯框架，为后文LDA两层贝叶斯框架的推导铺垫。贝叶斯学派认为词的生成不止一层：词的概率分布有很多种，即概率分布本身也服从一种概率分布，就像是上帝有许多骰子，他挑选了一个骰子再扔，生成了词。

• 也就是说，Unigram模型下一篇文档只是一袋子词，这些词的生成遵循一个分布，设为\(\mathop{p}^{\rightarrow}\)，同时这个词生成分布也遵循一个分布，设为\(p(\mathop{p}^{\rightarrow})\)。用数学公式把上面说的两层分布翻译下，就是一篇文档的生成概率：

  \[ p(W)=\int p(W|\mathop{p}^{\rightarrow})p(\mathop{p}^{\rightarrow})d\mathop{p}^{\rightarrow} \]

• 按照贝叶斯学派的观点，我们应该先假设一个先验分布，再用训练数据修正它，此处我们需要假设\(p(\mathop{p}^{\rightarrow})\)，也就是分布的分布的先验，训练数据是什么？是我们从语料中提取的词频分布，假设\(\mathop{n}^{\rightarrow}\)是所有词的词频序列，则这个序列满足多项分布：

  \[ \begin{aligned} p(\mathop{n}^{\rightarrow}) &= Mult(\mathop{n}^{\rightarrow}|\mathop{p}^{\rightarrow},N) \\ &= C_N ^{\mathop{n}^{\rightarrow}} \prod_{k=1}^V p_k^{n_k} \\ \end{aligned} \]

• 既然训练数据满足多项分布，我们自然而然想利用Dirichlet-Multinomial共轭，因此假设\(p(\mathop{p}^{\rightarrow})\)的先验分布为Dirichlet分布：

  \[ Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow})=\frac{1}{\int \prod_{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow}} \prod_{k=1}^V p_k^{\alpha _k -1} \]

  其中\(V\)是语料词典大小，Dirichlet分布的参数\(\alpha\)需要自己设置。之后根据共轭得到数据修正之后\(p(\mathop{p}^{\rightarrow})\)的后验分布：

  \[ \begin{aligned} p(\mathop{p}^{\rightarrow}|W,\mathop{\alpha}^{\rightarrow}) &= Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow})+MultCount(\mathop{n}^{\rightarrow}) \\ &= Dir(\mathop{p}^{\rightarrow}|\mathop{\alpha}^{\rightarrow}+\mathop{n}^{\rightarrow}) \\ \end{aligned} \]

• 得到后验之后，可以使用极大似然估计或者均值估计来计算\(\mathop{p}^{\rightarrow}\)，这里我们使用后验里Dirichlet分布的均值来估计，结合之前提到了Dirichlet的性质，有：

  \[ \mathop{p_i}^{~}=\frac{n_i+\alpha _i}{\sum _{i=1}^{V} (n_i+\alpha _i)} \]

  这个式子的物理解释：不同于一般的使用词频作为估计，我们首先假设了词频（即先验的伪计数\(\alpha _i\)），然后加上数据给出的词频\(n_i\)，再归一化作为概率。

• 现在得到了词语的生成概率分布\(\mathop{p}^{\rightarrow}\)，那么在此分布下的文档的生成概率显然为：

  \[ p(W|\mathop{p}^{\rightarrow})=\prod _{k=1}^V p_k^{n_k} \]

  将词生成概率分布的分布，文档在词生成分布下的条件生成概率带入之前提到的文档概率积分式，就得到所有分布情况下，文档的生成概率。代入化简之后可以得到一个很漂亮的式子。

  \[ p(W|\mathop{\alpha}^{\rightarrow})=\frac{\Delta(\mathop{\alpha}^{\rightarrow}+\mathop{n}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \]

  其中\(\Delta\)是归一化因子：

  \[ \Delta(\mathop{\alpha}^{\rightarrow})=\int \prod _{k=1}^V p_k^{\alpha _k -1}d\mathop{p}^{\rightarrow} \]

PLSA模型

• PLSA即概率隐含语义分析模型，这个模型认为文档到词之间存在一个隐含的主题层次，文档包含多个主题，每个主题对应一种词的分布，生成词时，先选主题，再从主题中选词生成（实际计算时是各个主题的概率叠加）。
• 与没有贝叶斯的unigram模型相比，plsa在文档和词之间加了一层，主题。
• PLSA没有引入贝叶斯，只是一个包含隐变量的模型，做最大似然估计，那么可以用EM算法迭代学习到参数，具体的计算在这里就略过了。

Role in LDA

• 现在整理一下，Unigram模型中主要包含两部分
  • 词生成概率分布
  • 词生成概率分布的参数分布
• PLSA模型主要包含两部分
  • 词生成概率分布
  • 主题生成概率分布
• Unigram模型展示了分布的分布，即为词分布引入参数先验的意义：使得词的分布是一个变量，从掷色子选出一个词变成了先选一个色子，再掷色子选词。至于引入先验究竟有没有用是贝叶斯学派和频率学派之间争吵的话题了。
• PLSA模型为人类语言生成提供了一个很直观的建模，引入了主题作为隐含语义，并定义了主题代表词的分布，将文章看成是主题的混合。

LDA文本建模

模型概述

• LDA整合了Unigram和PLSA的优点，对于词和主题这两个骰子分别加上了Dirichlet先验假设
  • 词生成概率分布（暂记A）
  • 词生成概率分布的参数分布（暂记B）
  • 主题生成概率分布（暂记C）
  • 主题生成概率分布的参数分布（暂记D）
• 这里初学容易混淆的是，主题生成概率分布并不是词生成概率分布的参数分布，要区分LDA模型中的层次关系和各个层次里共轭关系。另外主题和词并不是一对多的层次关系，两者是多对多的关系，事实上，在LDA模型中一篇文档是这么生成的（假设有K个主题)：
  • 先在B分布条件下抽样得到K个A分布
  • 对每一篇文档，在符合D分布条件下抽取得到一个C分布，重复如下过程生成词：
    • 从C分布中抽样得到一个主题z
    • 从第z个A分布中抽样得到一个单词
• 假设有\(m\)篇文档，\(n\)个词，\(k\)个主题，则\(D+C\)是\(m\)个独立的Dirichlet-Multinomial共轭，\(B+A\)是\(k\)个独立的Dirichlet-Multinomial共轭。两个dirichlet参数分别为1个k维向量(\(\alpha\))和1个n维向量(\(\beta\))。现在我们可以理解本文最开始的配图，我们将符号用其实际意义表述，与标题配图对应，这幅图实际上描述了LDA中这\(m+k\)个独立的Dirichlet-Multinomial共轭：

建立分布

• 现在我们可以用\(m+k\)个Dirichlet-Multinomial共轭对LDA主题模型建模了，借鉴之前推导Unigram模型时得到最终的文档生成分布，我们可以分别计算：

  \[ \begin{aligned} p(\mathop{z}^{\rightarrow}|\mathop{\alpha}^{\rightarrow}) = \prod _{m=1}^M \frac{\Delta(\mathop{n_m}^{\rightarrow}+\mathop{\alpha}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \\ p(\mathop{w}^{\rightarrow}|\mathop{z}^{\rightarrow},\mathop{\beta}^{\rightarrow}) = \prod _{k=1}^K \frac{\Delta(\mathop{n_k}^{\rightarrow}+\mathop{\beta}^{\rightarrow})}{\Delta(\mathop{\beta}^{\rightarrow})} \\ \end{aligned} \]

• 最终得到词与主题的联合分布:

  \[ p(\mathop{w}^{\rightarrow},\mathop{z}^{\rightarrow}|\mathop{\alpha}^{\rightarrow},\mathop{\beta}^{\rightarrow}) = \prod _{m=1}^M \frac{\Delta(\mathop{n_m}^{\rightarrow}+\mathop{\alpha}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \prod _{k=1}^K \frac{\Delta(\mathop{n_k}^{\rightarrow}+\mathop{\beta}^{\rightarrow})}{\Delta(\mathop{\beta}^{\rightarrow})} \]

采样

• 在前面说了，我们按照贝叶斯推断的框架估计模型参数，需要直到主题分配的后验概率，这里就需要gibbs sampling来帮忙对后验做一个近似

• 按照gibbs sampling的定义，我们需要主题分配的完全条件概率\(p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})\)去采样，进而近似\(p(z_i=k|\mathop{w}^{\rightarrow})\)，\(z_i\)代表第i个词的主题（这里下标i代表第m篇文档第n个词），而向量w代表我们现在观察到的所有词。

• 在建立了整个概率模型之后，我们通过以下方法训练：设定好超参，随机初始化各个词频统计（包括文章m下主题k的词数，词汇t属于主题k的词数，文章m的总词数，主题k的总词数），然后对语料中所有词，依次进行吉布斯采样，采样其主题，并分配给该词这个主题，并更新四个词频（即利用共轭更新后验），循环采样直到收敛，即采样之后的主题分布基本符合后验概率下的模型产生的主题分布，数据已经不能提供给模型更多的知识（不再进行更新）。

  • 其中吉布斯采样是需要限定某一维，按照其他维度的条件概率进行采样，在文本主题建模中维度就是词语，按其他维度的条件概率计算就是在四个词频中除去当前词语及其主题的计数。
  • 采样后主题后将这个主题分配给词语，四个词频计数增加，如果已经收敛，则采样前后主题相同，词频没有改变，则相当于后验没有从数据知识中获得更新。

• 公式推导：下面分别介绍两种推导方法，第一种是LDA数学八卦一文中基于共轭关系做出的推导，另一种是Parameter estimation for text analysis 一文中基于联合分布做出的推导

• 基于共轭关系推导如下：

• 采样的对象是词所对应的主题，概率为：

  \[ p(z_i=k|\mathop{w}^{\rightarrow}) \]

• 使用吉布斯采样来采样某一个词的主题，则需要用其他词的主题作为条件计算条件概率：

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow}) \]

• 由贝叶斯公式，这个条件概率正比于（采样我们可以按正比扩大各个概率采样）：

  \[ p(z_i=k,w_i=t|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow}) \]

• 把这个公式按主题分布和词分布展开：

  \[ \int p(z_i=k,w_i=t,\mathop{\vartheta _m}^{\rightarrow},\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\vartheta _m}^{\rightarrow} d\mathop{\varphi _k}^{\rightarrow} \]

• 由于所有的共轭都是独立的，上式可以写成：

  \[ \int p(z_i=k,\mathop{\vartheta _m}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})p(w_i=t,\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\vartheta _m}^{\rightarrow} d\mathop{\varphi _k}^{\rightarrow} \]

• 把概率链式分解下，又因为两个式子分别和主题分布和词分布相关，因此可以写成两个积分相乘：

  \[ \int p(z_i=k|\mathop{\vartheta _m}^{\rightarrow})p(\mathop{\vartheta _m}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\vartheta _m}^{\rightarrow} \cdot \int p(w_i=t|\mathop{\varphi _k}^{\rightarrow})p(\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})d\mathop{\varphi _k}^{\rightarrow} \]

• 已知第m篇文档的主题分布和第k个主题词分布，求第i个词为t的概率和第i个词对应主题为k的概率，那么显然：

  \[ p(z_i=k|\mathop{\vartheta _m}^{\rightarrow})=\mathop{\vartheta _{mk}} \\ p(w_i=t|\mathop{\varphi _k}^{\rightarrow})=\mathop{\varphi _{kt}} \\ \]

• 而根据共轭关系，有

  \[ p(\mathop{\vartheta _m}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})=Dir(\mathop{\vartheta _m}^{\rightarrow}|\mathop{n_{m,¬ i}}^{\rightarrow}+\mathop{\alpha}^{\rightarrow}) \\ p(\mathop{\varphi _k}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w_{¬ i}}^{\rightarrow})=Dir(\mathop{\varphi _k}^{\rightarrow}|\mathop{n_{k,¬ i}}^{\rightarrow}+\mathop{\beta}^{\rightarrow}) \\ \]

• 因此整个式子可以看作是两个Dirichlet分布的期望向量的第k项和第t项相乘。而根据之前Dirichlet的性质，易得这两个期望是按Dirichlet参数比例得到的分式，因此最后的概率计算出来就是（注意是正比于）：

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})∝\frac{n_{m,¬ i}^{(k)}+\alpha _k}{\sum _{k=1}^K (n_{m,¬ i}^{(k)}+\alpha _k)} \cdot \frac{n_{k,¬ i}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k,¬ i}^{(t)}+\beta _t)} \]

• 这个概率可以理解为（排除当前这第i个token以外）：

  \[ (文档m中主题k所占的比例) * (主题k中词t所占的比例） \]

• 注意到第一项的分母是对主题求和，实际上和k无关，因此可以写成：

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})∝ (n_{m,¬ i}^{(k)}+\alpha _k) \cdot \frac{n_{k,¬ i}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k,¬ i}^{(t)}+\beta _t)} \]

• 我们再看看基于联合分布如何推导

• 之前我们已经得到词和主题的联合分布：

  \[ p(\mathop{w}^{\rightarrow},\mathop{z}^{\rightarrow}|\mathop{\alpha}^{\rightarrow},\mathop{\beta}^{\rightarrow}) = \prod _{m=1}^M \frac{\Delta(\mathop{n_m}^{\rightarrow}+\mathop{\alpha}^{\rightarrow})}{\Delta(\mathop{\alpha}^{\rightarrow})} \prod _{k=1}^K \frac{\Delta(\mathop{n_k}^{\rightarrow}+\mathop{\beta}^{\rightarrow})}{\Delta(\mathop{\beta}^{\rightarrow})} \]

• 根据贝叶斯公式有

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})=\frac{p(\mathop{w}^{\rightarrow},\mathop{z}^{\rightarrow})}{p(\mathop{w}^{\rightarrow},\mathop{z_{¬ i}}^{\rightarrow})} \\ =\frac{p(\mathop{w}^{\rightarrow}|\mathop{z}^{\rightarrow})} {p(\mathop{w_{¬ i}}^{\rightarrow}|\mathop{z_{¬ i}}^{\rightarrow})p(w_i)} \cdot \frac{p(\mathop{z}^{\rightarrow})} {\mathop{p(z_{¬ i})}^{\rightarrow}} \\ \]

• 因为\(p(w_i)\)是可观测变量，我们省略它，得到一个正比于的式子，将这个式子用之前的\(\Delta\)形式表示（分式除以分式，分母相同抵消了）：

  \[ ∝ \frac{\Delta(\mathop{n_{z}}^{\rightarrow})+\mathop{\beta}^{\rightarrow}}{\Delta(\mathop{n_{z,¬ i}}^{\rightarrow})+\mathop{\beta}^{\rightarrow}} \cdot \frac{\Delta(\mathop{n_{m}}^{\rightarrow})+\mathop{\alpha}^{\rightarrow}}{\Delta(\mathop{n_{m,¬ i}}^{\rightarrow})+\mathop{\alpha}^{\rightarrow}} \]

• 将\(\Delta\)的表达式带入计算，也可以得到：

  \[ p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})∝ (n_{m,¬ i}^{(k)}+\alpha _k) \cdot \frac{n_{k,¬ i}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k,¬ i}^{(t)}+\beta _t)} \]

• 最后附上Parameter estimation for text analysis一文中吉布斯采样的伪算法图：

i0oU6U.png

• 可以看到主要通过记录四个n值（两个矩阵两个向量）来计算条件概率，更新主题时也是更新四个n值进行增量更新。算法先通过随机均匀采样赋初值，然后按采样公式更新主题（先减去旧的主题分配，再加上新的主题分配），其中公式78即之前我们计算得到的\(p(z_i=k|\mathop{z_{¬ i}}^{\rightarrow},\mathop{w}^{\rightarrow})\)，公式81和82分别为\(\mathop{\vartheta _{mk}},\mathop{\varphi _{kt}}\)，我们可以直接通过四个n值得到，不用考虑采样时的\(¬ i\)条件了，具体是：

  \[ \mathop{\vartheta _{mk}} = \frac{n_{m}^{(k)}+\alpha _k}{\sum _{k=1}^K (n_{m}^{(t)}+\alpha _k)} \\ \mathop{\varphi _{kt}} = \frac{n_{k}^{(t)}+\beta _t}{\sum _{t=1}^V (n_{k}^{(t)}+\beta _t)} \]

训练与测试

• 接下来我们来训练LDA模型，首先对LDA的Dir参数随机初始化（先验），然后使用文本进行数据知识补充，得到最终正确的后验，训练是一个迭代过程：
  • 迭代什么？采样并更新词对应的主题
  • 根据什么迭代？gibbs采样的完全条件概率
  • 迭代之后的效果？主题分配改变、统计量改变、下一次gibbs采样的完全条件概率改变
  • 迭代到什么时候为止？Gibbs采样收敛，即采样一段时间区间内主题分布稳定不变，或者根据困惑度等指标来衡量模型收敛的程度。
• 训练和测试的区别在于，训练是针对全文档集进行采样更新，文档到主题和主题到词的分布都在更新，而测试则保留主题到词的分布不变，只针对当前测试的文档采样到收敛，得到该文档的主题分布。
• 事实上两个超参\(\alpha\)和\(\beta\)在训练完之后是经过了很多次后验替换先验的迭代，参数值很大了，\(\alpha\)就抛弃了这最后的后验结果，在对新文档产生主题分布时重新用最开始的先验值，这样的话中途得到的训练集上的文档到主题的分布在测试新文档时实际上是用不上的，我们利用的是主题到词的分布：因为只有主题集合是针对整个文档空间的（训练集和测试集），主题到词的分布也是建立在整个文档空间的词典上的，这一部分的k个\(\beta\)向量我们保留最后的后验结果，因为这个后验吸收了数据的似然知识后参数值很大，不确定度很小了，基本上每个\(\beta\)向量就等同于确定了一个主题到词的多项式分布，也就是确定了一个主题。我们利用这确定的主题，来测试一篇新文档在各个主题上的分布。因此在测试新文档时参数\(\alpha\)一般设置为对称的，即各个分量相同（没有先验偏好那个主题），且值很小（即不确定度大，否则生成的主题分布是均匀分布），这里类似于最大熵的思想。测试是利用已知的固定的主题去得到文档到主题的分布。
• LDA的训练实际上是一种无参贝叶斯推断，可以采用MCMC方法和非MCMC方法，MCMC方法中经常采用的就是Gibbs采样，而非MCMC方法还可以用变分推断等方法来迭代得到参数。

LDA in Gensim

• Gensim中的LDA提供了几个参数，其中\(\alpha\)的默认值如下：

  alpha ({numpy.ndarray, str}, optional) – Can be set to an 1D array of length equal to the number of expected topics that expresses our a-priori belief for the each topics’ probability. Alternatively default prior selecting strategies can be employed by supplying a string: ’asymmetric’: Uses a fixed normalized asymmetric prior of 1.0 / topicno. ’default’: Learns an asymmetric prior from the corpus.

  Gensimmodels.ldamodel – Latent Dirichlet Allocation

• gensim中没有暴露\(\beta\)给用户，用户只能设置\(\alpha\)，可以自定义，也可以设置对称或者不对称。其中对称设置即全为1，不对称设置则拟合了zipf law（？），可能\(\beta\)的默认设置就是不对称。

More

• Parameter estimation for text analysis 一文指出了隐主题实际上来自词与词之间的高阶共现关系

• LDA用于document query，其中LDA在candidates上训练，新来一个query就进行一次测试

  • 基于similarity ranking的方法，使用JS距离或者KL散度计算candidate与query之间topic distribution的相似度，并排序

  • 基于Predictive likelihood ranking的方法，计算给定query，每个candidate出现的概率，基于主题z分解：

    \[ \begin{aligned} p\left(\vec{w}_{m} | \tilde{\vec{w}}_{\tilde{m}}\right) &=\sum_{k=1}^{K} p\left(\vec{w}_{m} | z=k\right) p\left(z=k | \tilde{\vec{w}}_{\tilde{m}}\right) \\ &=\sum_{k=1}^{K} \frac{p\left(z=k | \vec{w}_{m}\right) p\left(\vec{w}_{m}\right)}{p(z=k)} p\left(z=k | \tilde{\vec{w}}_{\tilde{m}}\right) \\ &=\sum_{k=1}^{K} \vartheta_{m, k} \frac{n_{m}}{n_{k}} \vartheta_{\tilde{m}, k} \end{aligned} \]

• LDA用于聚类

  • 事实上主题分布就是对文档的一种软聚类划分，假如把每篇文档划分到拥有最大概率的主题上的话，那就是一种硬划分。
  • 或者利用topic distribution作为文档的特征向量，再进一步使用各种聚类算法聚类
  • 聚类结果的评估，可以利用一个已知聚类划分的结果作为参考，利用Variation of Information distance进行评估

• LDA的评价指标，困惑度，其定义为模型在验证集上测出的似然的reciprocal geometric mean：

  \[ \mathrm{P}(\tilde{\boldsymbol{W}} | \boldsymbol{M})=\prod_{m=1}^{M} p\left(\tilde{\vec{w}}_{\tilde{m}} | \mathcal{M}\right)^{-\frac{1}{N}}=\exp -\frac{\sum_{m=1}^{M} \log p\left(\tilde{\bar{w}}_{\tilde{m}} | \mathcal{M}\right)}{\sum_{m=1}^{M} N_{m}} \]

• 假定验证集和训练集分布一致，那么LDA在验证集上的困惑度高，代表熵越大，不确定性大，模型还没有学到一个稳定的参数。