Paper Reading 2

- Distractor Mechanism
- External Information Attention
- Pointer Copy Network PGNet
- Extractive Summary Based on RNN
- Transformer
- Selection gate mechanism

Distraction-Based Neural Networks for Document Summarization
Not only using attention mechanisms but also attention dispersion mechanisms to better capture the overall meaning of the document. Experiments have shown that this mechanism is particularly effective when the input is long text.
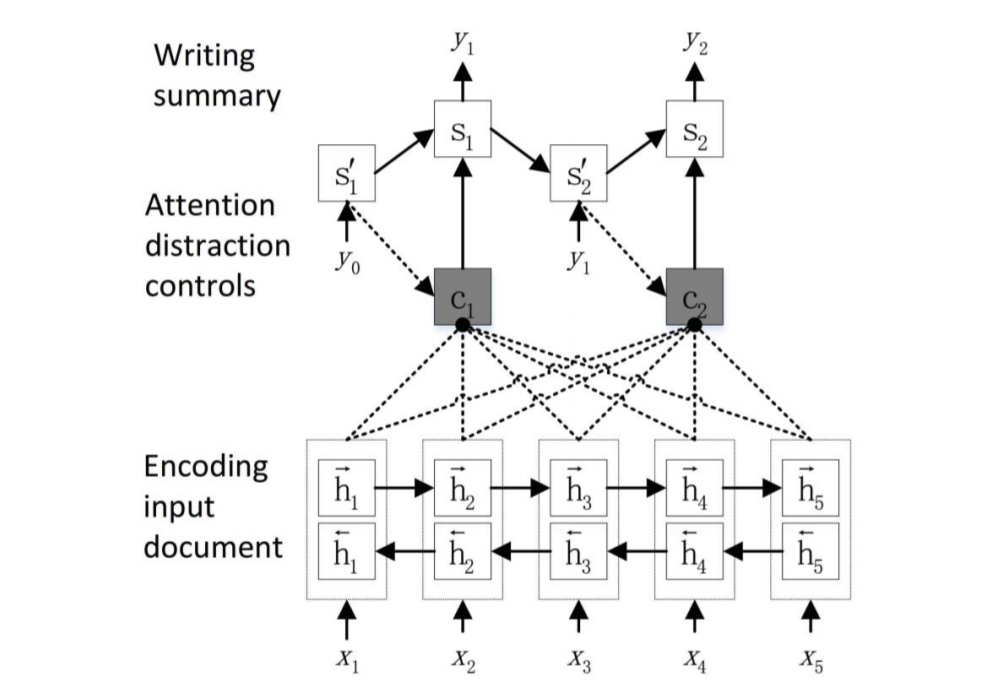
![i0oh0H.png]()
Introducing a control layer between the encoder and decoder to achieve attention concentration and attention dispersion, using two layers of GRU:
This control layer captures the connection between $st^{‘}$ and $c_t$ , where the former encodes the current and previous output information, and the latter encodes the current input that has been processed through attention focusing and attention dispersion, while $e(y{t-1})$ is the embedding of the previous input.
Three Attention Diversion Models
M1: Calculate c_t for the control layer, distribute it over the inputs, where c_t is the context c_t^{temp} encoded by a standard attention mechanism, obtained by subtracting the historical context, similar to a coverage mechanism
M2: Distribute the attention weights, similarly, subtract the historical attention and then normalize
M3: Perform dispersion at the decoding end, calculate the distances between the current $c_t$ , $s_t$ , $\alpha _t$ , and the historical $c_t$ , $s_t$ , $\alpha _t$ , and output the probabilities together as the scores relied on during the 束 search during decoding.
Document Modeling with External Attention for Sentence Extraction
- A retrieval-based summarization model was constructed, consisting of a hierarchical document encoder and an extractor based on external information attention. In the summarization task, the external information is image captions and document titles.
- By implicitly estimating the local and global relevance of each sentence to the document and explicitly considering external information, it determines whether each sentence should be included in the abstract.
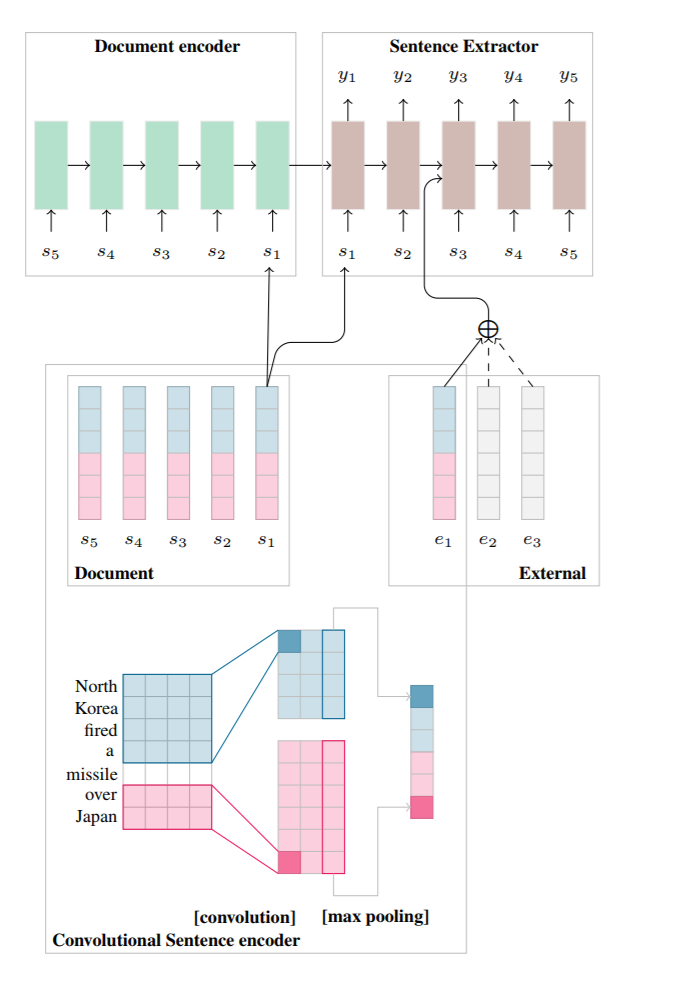
- Sentence-level Encoder: As shown in the figure, using CNN encoding, each sentence is encoded with three convolutional kernels of sizes 2 and 4 respectively, and the resulting vectors are subjected to maxpooling to generate a single value, thus the final vector is 6-dimensional.
- Document-level encoder: Input the 6-dimensional vector of a document’s sentence sequentially into LSTM for encoding.
- Sentence Extractor: Composed of an LSTM with attention mechanism, unlike the general generative seq2seq, the encoding of the sentence is not only used as the encoding input in the seq2seq but also as the decoding input, with one being in reverse order and the other in normal order. The extractor relies on the encoding side input $s_t$ , the previous time step state on the decoding side $h_t$ , and the attention-weighted external information $h_t^{‘}$ .
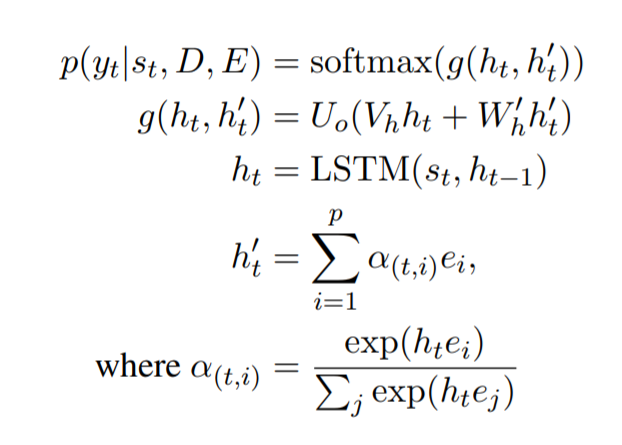
Get To The Point: Summarization with Pointer-Generator Networks
Presented two mechanisms, Pointer-Generator addresses the OOV problem, and coverage resolves the issue of repeated words
Pointer-Generator: Learning pointer probabilities through context, the decoder state of the current timestep, and input
Pointer probability indicates whether a word should be normally generated or sampled from the input according to the current attention distribution, in the above formula. If the current label is OOV, the left part is 0, maximizing the right part to allow the attention distribution to indicate the position of the copied word; if the label is a newly generated word (not mentioned in the original text), the right part is 0, and maximizing the left part means generating words normally using the decoder. Overall, it learns the correct pointer probability.
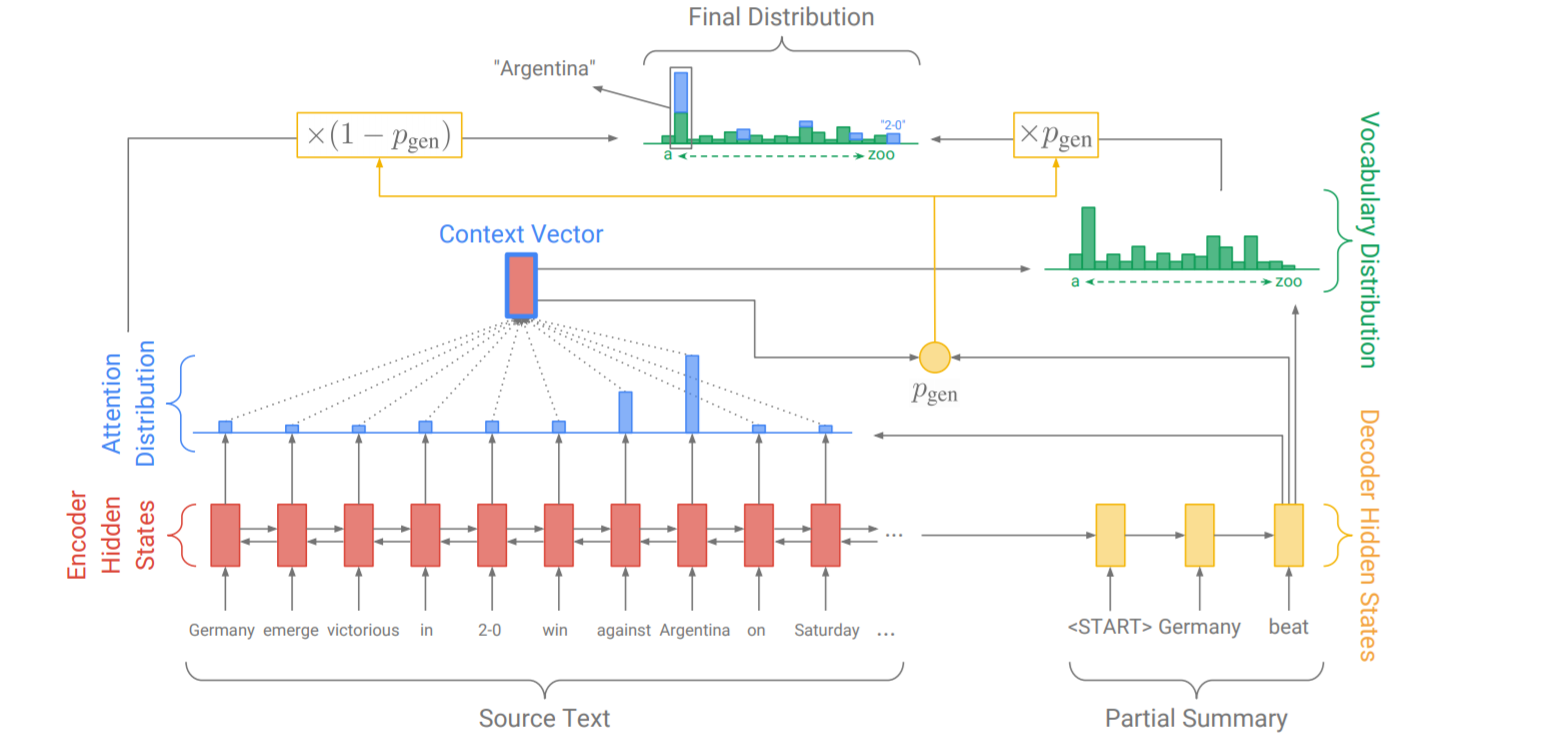
Coverage: Utilizing the coverage mechanism to adjust attention, so that words that received more attention in previous timesteps receive less attention
Common Attention Calculation
Maintain a coverage vector indicating how much attention each word has received prior to this:
Then use its corrected attention generation to make the attention generation consider the previous accumulated attention
And add a coverage loss to the loss function
The use of min means that we only penalize the overlapping parts of the attention and coverage distributions, i.e., if coverage is large and attention is also large, then covloss is large; if coverage is small, regardless of the attention, covloss is small
SummaRuNNer: A Recurrent Neural Network based Sequence Model for Extractive Summarization of Documents
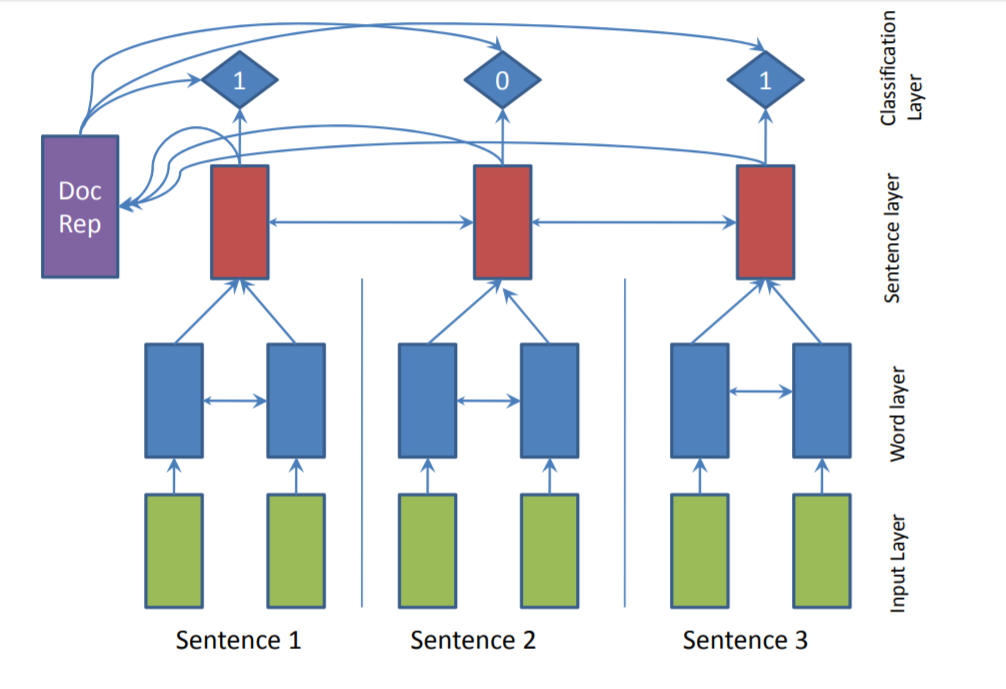
Using RNN for extractive summarization, the model decision process can be visualized, and an end-to-end training method is employed
Treat extraction as a sentence classification task, visit each sentence in the order of the original text, and decide whether to include it in the abstract, with this decision considering the results of previous decisions.
Encoding at the word level using a bidirectional GRU, followed by encoding at the sentence level using another bidirectional GRU; the encodings from both layers are concatenated in reverse order and then averaged through pooling
d is the encoding of the entire document, $h_j^f$ and $h_j^b$ represent the forward and reverse encodings of the sentence through GRU
Afterward, a neural network is trained for binary classification based on the coding of the entire document, the coding of the sentences, and the dynamic representation of the abstract at the current sentence position, to determine whether each sentence should be included in the abstract:
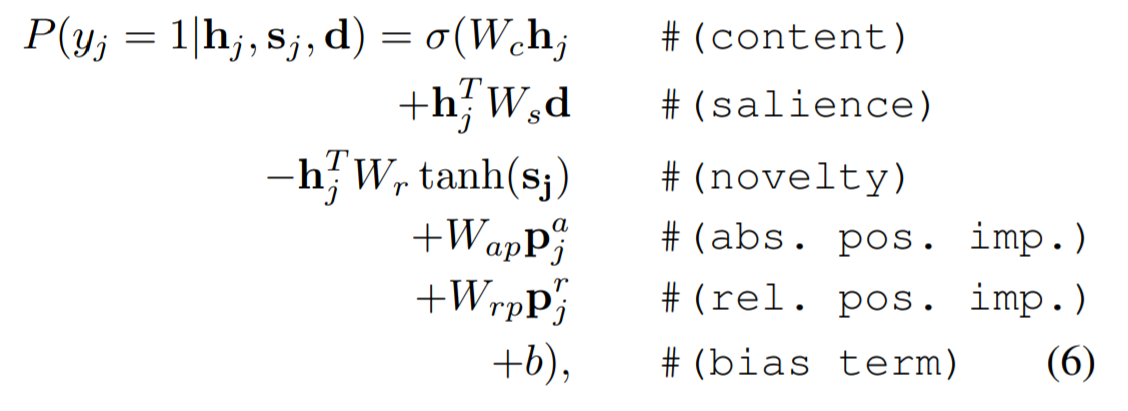
sj represents the abstraction generated up to position j, obtained by weighted summation of the encoding of previous sentences using the binary classification probability of each sentence:
First line: The parameter is the encoding of the current sentence, representing the content of the current sentence
Second line: Parameters are document encoding and sentence encoding, indicating the significance of the current sentence to the document
Third line: The parameters are the sentence encoding and the dynamic encoding of the summary, indicating the redundancy of the current sentence to the generated summary.
Fourth and fifth lines: Considered the relative and absolute positions of sentences within the document. (The absolute position denotes the actual sentence number, whereas the relative position refers to a quantized representation that divides each document into a fixed number of segments and computes the segment ID of a given sentence.)
Finally, perform the maximum likelihood estimation on the entire model:
The author applies this extraction method to generative summarization corpora, that is, how to label each sentence in the original text with a binary classification. The author believes that the subset of sentences labeled as 1 should correspond to the maximum ROUGE value of the generative summary, but finding all subsets is too time-consuming, so a greedy method is used: sentences are added one by one to the subset, and if no remaining sentence can increase the ROUGE value of the current subset, it is not added. In this way, the generative summarization corpora are converted into extraction summarization corpora.
Another approach is to train directly on the generative abstract corpus, taking the dynamic abstract representation mentioned above, specifically the last sentence which contains the entire document’s abstract representation s, and inputting it into a decoder to generate the generative abstract. Since the abstract representation is the only input to the decoder, training the decoder also allows learning good abstract representations, thereby completing the task of extractive summarization.
Because several components are included in generating the binary classification probabilities, normalizing them allows for the visualization of the contributions made by each component, thereby illustrating the decision-making process:

Attention Is All You Need
- Abandoned RNN and CNN for seq2seq tasks, directly using multi-head attention to compose network blocks and stack them, adding BN layers and residual connections to construct a deep network
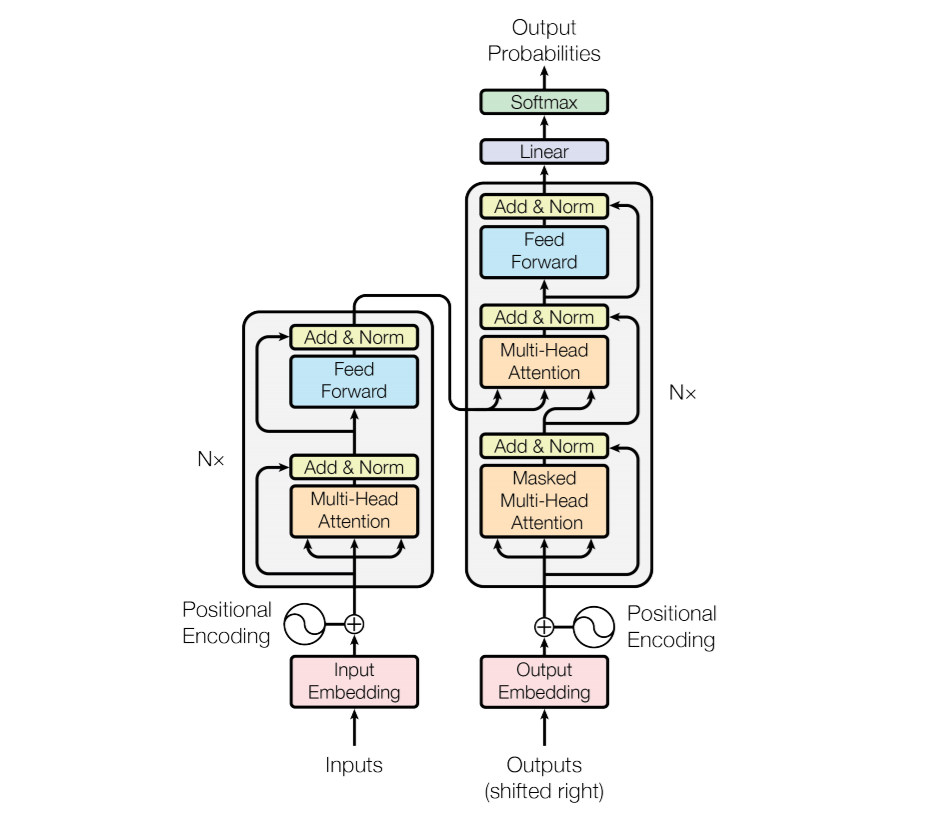
- The benefit of using attention exclusively is speed.
- In order to utilize residuals, all submodules (multi-head attention and fully connected) are unified to output dimensions of 512
- Encoding end: 6 blocks, each containing an attention and a fully connected sub-module, both using residuals and batch normalization.
- Decoder side: Also consists of 6 blocks, the difference being the addition of an attention mechanism to process the output from the encoding side, and the attention mechanism connected to the decoder input uses a mask to ensure directionality, that is, the output at the i-th position is only related to the output at previous positions.
- The six blocks of encoding and decoding are all stacked (stacked)
- The general attention model refers to a mechanism that maps a query and a series of key-value pairs to an output, where the output is a weighted sum of the values, and the weight of each value is calculated by a compatibility function corresponding to the key and the query input. The traditional attention keys and values are the same, both being the hidden layer states at each input position, with the query being the current output, and the compatibility function being various attention calculation methods. The three arrows pointing to attention in the diagram represent key, value, and query respectively.
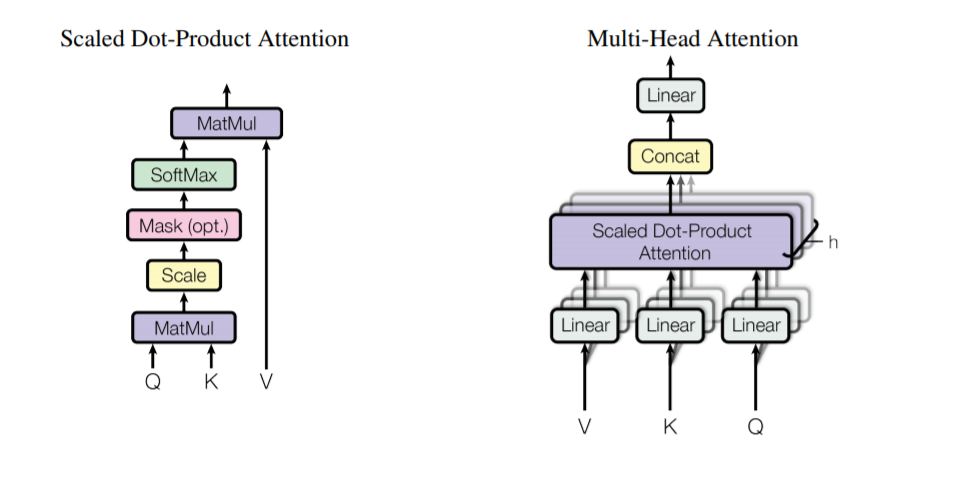
Multi-head attention is composed of multiple parallel scaled dot-product attention mechanisms.
Scaled dot-product attention, as shown, first performs a dot product between the query and key, then scales, and if it is the attention from the decoder input, a mask is added. After that, it passes through the softmax function to perform a dot product with the value to obtain the attention weights. In actual computation, to accelerate, a series of queries, keys, and values are calculated together, so Q, K, and V are all matrices. The scaling is to prevent the dot product attention from being at the ends of softmax when the dimension of k is too large, resulting in small gradients.
Multi-head attention is a scaled dot-product attention with h projections on V, K, and Q, learning different features, and finally concatenating and performing a linear transformation. The authors believe that this multi-head design allows the model to learn the information of representation subspaces at different positions.
In the paper, 8 heads are taken, and to ensure dimension consistency, the dimensions of individual q, k, and v are set to 512/8=64
This multi-head attention is used in three places in the model:
- -based attention mechanism.
- Self-attention between encoding blocks and blocks
- Decoding blocks and inter-block self-attention
In each block, there is also a fully connected layer, which contains two linear transformations, with ReLU activation inserted in between, and the same parameters are used at each input position, but the parameters of the fully connected layers in different blocks are different
The complete use of attention would discard the sequential order information of the sequence; to utilize this information, trigonometric positional encoding is added to make use of relative positional information:
A Joint Selective Mechanism for Abstractive Sentence Summarization
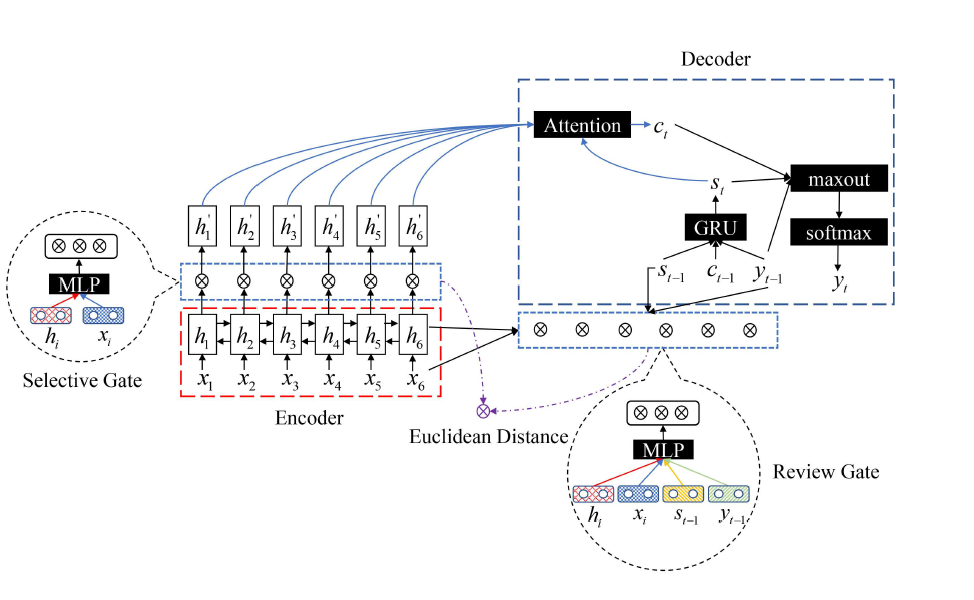
Abstracts differ from translations; end-to-end frameworks should model the loss (information compression) rather than simply align as translations do
The author made two improvements to loss modeling:
- After encoding is completed, a threshold is added for trimming the encoded information
- Added a selection loss, focusing on both input and output, to assist the threshold operation
The selection of the threshold considers both the hidden layer states after encoding and the original word embeddings, and acts upon the hidden layer states, truncating the hidden vectors before passing them through attention-weighted generation of context. The authors believe that this process is equivalent to allowing the network to observe the word embeddings before and after the rnn processing, thereby knowing which word in the input is important for generating the abstract:
The selection of the loss function constructs a review threshold at the decoding end, considering the hidden layers of the encoding end and the original input, the hidden layers of the decoding end and the original input, and the review threshold at each position of the decoding end is the average of the review thresholds at all positions of the encoding end:
The author believes that the role of the review threshold is equivalent to allowing the network reading to generate abstracts and to review the input text, so that it knows how to select abstracts.
Afterward, use the Euclidean distance with the selection threshold and review threshold as the selection loss, and add it to the total loss:
The author does not explain why the Euclidean distance between the review threshold and the selection threshold is taken as the loss function, nor does it clarify the distinction between the selection threshold and attention. It seems like a type of attention mechanism that considers the original input embedding, and it first trims each hidden layer at every time step before traditional attention weighting. The selected visual examples are also very clever, precisely demonstrating that this selection mechanism can identify shifts in sentences, thus changing the selected words, which contrasts with the original paper proposing the selection threshold, Selective Encoding for Abstractive Sentence Summarization. The original paper also does not explain the motivation for this design.