Lagrange,KKT,PCA,SVM

---

Introduction of the Lagrange multiplier method and its extension KKT conditions, as well as their applications in PCA and SVM

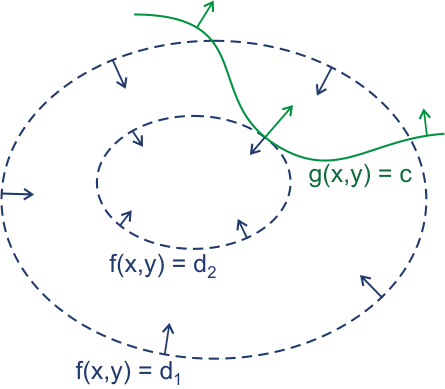
Image from Wikipedia's illustrative introduction to the Lagrange multiplier method

切换中文

Lagrange multiplier method

• Lagrange multiplier method is a method for finding extrema under constraints, described as

  \[ under the constraint condition g(x,y)=c \\ find the extremum of f(x,y) \\ \]

  The main idea is to synthesize the constraint conditions and the original function into a single function, convert it into an unconstrained condition, and then find the partial derivatives to obtain the extremum.

• It can be seen from the figure that points with equal values of the function f can form blue rings similar to contour lines, with the constraint conditions represented by the green path. The problem can be transformed into finding the point along the green path where the blue ring associated with that point is either closest to the center or farthest from the center (maximum or minimum value).

• Clearly, the point of tangency between the green path and the blue loop attains an extremum, at which their gradients (arrows) are parallel, described as

  \[ \nabla f (x, y) = \nabla (\lambda \left(g \left(x, y \right) - c \right)) \]

  \(\lambda\) is the Lagrange multiplier, representing the size multiple of the two parallel gradients in this formula, with the sign indicating that the two gradients are in opposite directions. The Lagrange multiplier is not equal to 0. The Lagrange equation is given by \(F(x,y)=\nabla \Big[f \left(x, y \right) + \lambda \left(g \left(x, y \right) - c \right) \Big]\)

• Solving the above equation yields a set of \((x,y,\lambda)\) , which are the critical points and the Lagrange multipliers at the points of extremum. At this time, the Lagrange equations \(F(x,y)=f(x,y)\) hold, because when the extremum is achieved, the constraint condition part must be 0 (we are moving along the constraint condition to find the tangent points, and the tangent points are on the constraint path).

• Lagrange coefficients refer to the maximum growth value, \(-\frac{\partial \Lambda}{\partial {c_k}} = \lambda_k\)

Carroll-Kuhn-Tucker condition

• If the constraint conditions are not only equations but also include inequality constraints, it is necessary to generalize the Lagrange multiplier method to the KKT conditions

• The problem of optimization with inequality constraints is described as

  \[ under the constraint condition: \\ h_j(X)=0 j=1,2,...,p \\ g_k(X)\leq 0 k=1,2,...q \\ find the extremum of f(X) \\ \]

• Lagrange function is

  \[ L(X,\lambda ,\mu)=f(X)+\sum _{j=1}^p \lambda _j h_j(X) + \sum _{k=1}^q \mu g_k(X) \]

• KKT conditions are given by:

  \[ \frac{dL}{dX}=0 \\ \lambda _j \neq 0 \\ \mu _k \geq 0 \\ \mu _k g_k(X)=0 \\ h_j(X)=0 \\ g_k(X) \leq 0\\ \]

PCA

• PCA stands for Principal Component Analysis, which optimizes the original dimensions of the data to form a set of new dimensions. These new dimensions are linear combinations of the original dimensions and are mutually independent. They are sorted by importance, with one dimension being understood as a column in a data matrix, where each row represents a sample

• \(x_1,...,x_p\) represents the original p dimensions, and the new dimensions are \(\xi _1,....,\xi _p\)

• New dimensions are linear combinations of the original dimensions, represented as

  \[ \xi _i = \sum _{j=1}^{p} \alpha _{ij} x_j = \alpha _i^T x \]

• In order to unify the scales across all new dimensions, the vector length of the coefficients of the linear combination of each new dimension is set to 1, i.e.,

  \[ \alpha _i^T \alpha _i=1 \]

• Let A be the feature transformation matrix, composed of the coefficient vectors of the linear combinations of the new dimensions, then it is necessary to solve for an optimal orthogonal transformation A such that the variance of the new dimensions reaches an extremum. An orthogonal transformation ensures that the new dimensions are uncorrelated; the greater the variance, the more distinct the samples are in the new dimensions, which facilitates our data classification.

• The problem is then transformed into an optimization problem with constraints, where the constraint is \(\alpha _i^T \alpha _i=1\) , and the extremum of \(var(\xi _i)\) is to be found, which can be solved using the Lagrange multiplier method

• When i=1, we obtain the first new dimension, which is also the most important (with the largest variance), and then set i=2, adding the constraint condition \(E[\xi _2 \xi _1\-E[\xi _1][\xi _2]]=0\) , that is, the two new dimensions are uncorrelated, and obtain the second new dimension

• Sequentially determine p new dimensions

• PCA can optimize the original data, identify dimensions with discriminative power, and more importantly, if there are correlations among the dimensions of the original data, PCA can eliminate these correlations. Even if the correlations in the original data are low, if we only take the first k (k < q) new dimensions, we can perform dimensionality reduction with minimal loss of precision, greatly shortening the training time of the data

• If we take the first k new dimensions and perform the inverse operation of PCA on them, we can achieve data denoising, because the new dimensions with very low importance generally reflect the random noise in the data. By discarding them and restoring the original data, we achieve the removal of noise

• PCA is unsupervised, does not consider the category or label of the samples themselves, and is not necessarily the optimal solution in supervised learning; feature extraction for classification objectives can be achieved using the K-L transform

PCA using Covariance Matrix

• The above method for solving PCA is too complicated; it can be solved through the covariance matrix in practice (because there are efficient matrix eigenvalue decomposition algorithms)
• The optimization objective of PCA is to reselect a set of bases (features) such that the covariance between different features is 0 under the representation of this set of bases, and the variance within the same feature is maximized
• The problem can be restated as, for the data tensor X, zero-centering by feature columns (a total of m features) (simplifying the calculation of covariance), calculate the covariance matrix \(C=\frac 1m X^T X\) . It is hoped to find a set of bases P such that the covariance matrix D of the transformed data \(Y=PX\) is diagonal, with non-diagonal elements (covariances) equal to 0. If the diagonal elements (variances) are arranged from large to small, then taking the first k rows of the P matrix can reduce the feature dimension from m to k. It is easy to obtain \(D=PCP^T\) , and since C is a real symmetric matrix, the problem then transforms into diagonalizing the real symmetric matrix C, and the new set of bases we need are the eigenvector set.
• Algorithm:

  • There are m sets of n-dimensional data arranged into a matrix X with n rows and m columns

  • Zero-mean normalization of each row of X

  • Determine the covariance matrix C

  • Determine the eigenvalues and eigenvectors of the covariance matrix

  • Arrange the feature vectors according to the size of their eigenvalues from largest to smallest in rows, forming a new basis matrix P

  • If necessary, take the first k rows of P, and the reduced-dimensional data is \(Y=PX\)

    def PCA(X, dims):
    m = len(X)
    mean = np.mean(X, axis=0)
    X = X - mean
    C = np.dot(X.T, X) / m
    Eigen_Value, Eigen_Vector = np.linalg.eig(C)
    index = np.argsort(Eigen_Value)[-1:-dims - 1:-1]
    PCA_Vector = Eigen_Vector[index]
    X_PCA = np.dot(PCA_Vector, X.T)
    return X_PCA.T

Support Vector Machine

• In classification learning, we need to find a separating hyperplane that separates samples of different categories, and the best separating hyperplane is obviously one that is as far away as possible from the samples of each category, i.e., the hyperplane with the best tolerance to local perturbations of the training samples

• The hyperplane is described by the equation \(w^Tx+b=0\) , where w is the normal vector determining the direction of the hyperplane, and b is the displacement of the hyperplane to the far point

• Solving an SVM, i.e., finding a solution that satisfies the constraints

  \[ \begin{cases} w^Tx_i+b \geq +1, y_i=+1 \\ w^Tx_i+b \leq -1, y_i=-1 \\ \end{cases} \]

  Under the given conditions, to maximize the distance \(\frac{2}{||w||}\) between two different support vectors to the hyperplane, which can be rewritten as an optimization problem

  \[ min_{w,b} \frac 12 {||w||}^2 \\ s.t. y_i(w^Tx_i+b) \geq 1,i=1,2,...,m \\ \]

  Derivation can be found in the other two blog posts: Machine Learning Notes and Statistical Learning Method Notes Handwritten Version

• For this optimization problem, its Lagrange equation is

  \[ L(w,b,\alpha )=\frac 12 {||w||}^2+\sum _{i=1}^{m} \alpha _i (1-y_i(w^Tx_i+b)) \]

  The term \(\alpha\) is the Lagrange multiplier, taking the partial derivatives of the equation with respect to w and b, obtaining the dual problem

  \[ max _{\alpha } \sum _{i=1}^m \alpha _i -\frac 12 \sum _{i=1}^m \sum _{j=1}^m \alpha _i \alpha _j y_i y_j x_i^T x_j \\ s.t. \sum _{i=1}^m \alpha _i y_i=0, \\ \alpha _i \geq 0,i=1,2,...,m \\ \]

  The above equation satisfies the KKT conditions, and is solved by the SMO algorithm

拉格朗日乘子法

• 拉格朗日乘子法是一种求约束条件下极值的方法，描述为

  \[ 在约束条件g(x,y)=c下 \\ 求函数f(x,y)的极值 \\ \]

  其主要思想是将约束条件和原函数合成一个函数，转换为无约束条件，进而求偏导得到极值。

• 由图可以看出，f函数值相等的点可以构成类似等高线的蓝色环，约束条件是绿色的路径。问题可以转换为，我们沿着绿色路径走，走到哪一点时这个点所在的蓝色环最靠中心或者最靠外沿(极大极小值)。

• 显然，在绿色路径与蓝色环相切的点取得极值，此时它们的梯度(箭头)平行，描述为

  \[ \nabla f (x, y) = \nabla (\lambda \left(g \left(x, y \right) - c \right)) \]

  \(\lambda\)是拉格朗日乘数，在这个式子中代表两个平行梯度的大小倍数，正负代表两个梯度方向相反。拉格朗日乘数不为0。 拉格朗日方程即$ F(x,y)=$

• 求解上面的式子，就得到一组\((x,y,\lambda)\)，即极值点和达到极值时的拉格朗日乘数。此时拉格朗日方程\(F(x,y)=f(x,y)\)，因为取得极值时约束条件部分一定为0(我们是沿着约束条件走找相切点，相切点在约束路径上)。

• 拉格朗日系数的含义是最大增长值，\(-\frac{\partial \Lambda}{\partial {c_k}} = \lambda_k\)

卡罗需-库恩-塔克条件

• 如果约束条件不仅仅是等式，还包括不等约束条件，这就需将拉格朗日乘子法推广到KKT条件

• 包含不等约束的极值问题描述为

  \[ 在约束条件: \\ h_j(X)=0 j=1,2,...,p \\ g_k(X)\leq 0 k=1,2,...q \\ 求函数f(X)的极值 \\ \]

• 拉格朗日函数为

  \[ L(X,\lambda ,\mu)=f(X)+\sum _{j=1}^p \lambda _j h_j(X) + \sum _{k=1}^q \mu g_k(X) \]

• KKT条件为:

  \[ \frac{dL}{dX}=0 \\ \lambda _j \neq 0 \\ \mu _k \geq 0 \\ \mu _k g_k(X)=0 \\ h_j(X)=0 \\ g_k(X) \leq 0\\ \]

PCA

• PCA即Principal Component Analysis，主成分分析，将数据原本的维度进行优化，形成一组新的维度，它们是原有维度的线性组合且互不相关，按重要性大小排序，一个维度可以理解为数据矩阵中一列，一行代表一个样本

• 记\(x_1,...,x_p\)为原始p个维度，新维度是\(\xi _1,....,\xi _p\)

• 新维度是原始维度的线性组合，表示为

  \[ \xi _i = \sum _{j=1}^{p} \alpha _{ij} x_j = \alpha _i^T x \]

• 为了各个新维度统一尺度，另每个新维度的线性组合系数的向量长度都为1，即

  \[ \alpha _i^T \alpha _i=1 \]

• 令A为特征变换矩阵，由各个新维度的线性组合系数向量构成，则需要求解一个最优的正交变换A，使得新维度的方差达到极值。其中正交变换即保证各个新维度不相关，方差越大则样本在新维度上具有区分度，方便我们进行数据的分类

• 此时问题就转化为具有约束条件的极值问题，约束条件为\(\alpha _i^T \alpha _i=1\)，求\(var(\xi _i)\)的极值，可以用拉格朗日乘子法求解

• 当i=1时，我们求出来第一个也是重要性最大(方差最大)的新维度，再令i=2,并加入约束条件\(E[\xi _2 \xi _1\-E[\xi _1][\xi _2]]=0\)即两个新维度不相关，求出第二个新维度

• 依次求出p个新维度

• PCA能够优化原始数据，找出具有区分度的维度，更重要的是如果原始数据的维度存在相关性，PCA能消除这些相关性，即便原始数据相关性很低，如果我们只取前k(k<q)个新维度，就可以在损失较小精确度的情况下进行降维，大大缩短数据的训练时间

• 如果我们取了前k个新维度，再对他们进行PCA的逆运算，就可以实现数据的降噪，因为重要性很低的新维度一般反应了数据中的随机噪声，抛弃它们并恢复原始数据时就实现了噪音的去除

• PCA是非监督的，没有考虑样本本身的类别或者标签，在监督学习中不一定是最优解，可以利用K-L变换实现针对分类的目标进行特征提取

PCA using Covariance Matrix

• 上述求解PCA的方法太过于麻烦，在实际中可以通过协方差矩阵来求解（因为有高效的矩阵特征分解算法）
• PCA的优化目标是，重新选取一组基（特征），使得数据在这组基表示下，不同特征之间的协方差为0，同一特征内的数据方差最大化
• 可以将问题转述为，对数据张量X，按特征列（共m个特征）零均值化（化简协方差的计算），计算协方差矩阵\(C=\frac 1m X^T X\)，希望求得一组基P，使得特征变换后的数据\(Y=PX\)的协方差矩阵D是对角阵，非对角元素（协方差）为0.若对角元素（方差）按从大到小排列，这时我们取P矩阵的前k行就可以将特征维度从m降到k。易得\(D=PCP^T\)，且C为实对称阵，那么问题就转变为对实对称C对角化，我们需要的新的一组基就是特征向量组。
• 算法：

  • 有m条n维数据，排成n行m列矩阵X

  • 将X的每一行进行零均值化

  • 求出协方差矩阵C

  • 求出协方差矩阵的特征值和特征向量

  • 将特征向量按特征值大小对应从大到小按行排列，组成新的基矩阵P

  • 如果需要将为，取P的前k行即可，降维后的数据为\(Y=PX\)

    def PCA(X, dims):
    m = len(X)
    mean = np.mean(X, axis=0)
    X = X - mean
    C = np.dot(X.T, X) / m
    Eigen_Value, Eigen_Vector = np.linalg.eig(C)
    index = np.argsort(Eigen_Value)[-1:-dims - 1:-1]
    PCA_Vector = Eigen_Vector[index]
    X_PCA = np.dot(PCA_Vector, X.T)
    return X_PCA.T

SVM

• 在分类学习中，我们需要找到一个划分超平面，将不同类别的样本分开，而最好的划分超平面显然是离所分各个样本类尽量远，即对训练样本局部扰动容忍性最好的超平面

• 划分超平面通过方程\(w^Tx+b=0\)描述，其中w为法向量，决定了超平面方向，b为超平面到远点的位移

• 求解一个SVM，即找到满足约束

  \[ \begin{cases} w^Tx_i+b \geq +1, y_i=+1 \\ w^Tx_i+b \leq -1, y_i=-1 \\ \end{cases} \]

  的条件下，使得两个异类支持向量到超平面的距离\(\frac{2}{||w||}\)最大 这可以重写为最优化问题

  \[ min_{w,b} \frac 12 {||w||}^2 \\ s.t. y_i(w^Tx_i+b) \geq 1,i=1,2,...,m \\ \]

  推导见另两篇博文：机器学习笔记和统计学习方法笔记手写版

• 对于这个最优化问题，它的拉格朗日方程是

  \[ L(w,b,\alpha )=\frac 12 {||w||}^2+\sum _{i=1}^{m} \alpha _i (1-y_i(w^Tx_i+b)) \]

  其中\(\alpha\)是拉格朗日乘子，令方程分别对w,b求偏导，得到对偶问题

  \[ max _{\alpha } \sum _{i=1}^m \alpha _i -\frac 12 \sum _{i=1}^m \sum _{j=1}^m \alpha _i \alpha _j y_i y_j x_i^T x_j \\ s.t. \sum _{i=1}^m \alpha _i y_i=0, \\ \alpha _i \geq 0,i=1,2,...,m \\ \]

  上式满足KKT条件，通过SMO算法求解