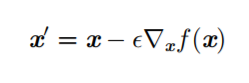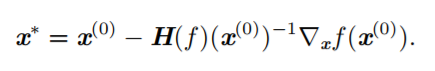Notes for ML

---

Notes on some concepts and algorithms in machine learning, sourced from:

• Elective Course on Pattern Recognition (An elective course for third-year students at Beijing University of Posts and Telecommunications, Pattern Recognition, textbook is "Pattern Recognition" compiled by Zhang Xuegong, published by Tsinghua University Press)
• Watermelon Book
• Statistical Learning Methods
• Deep Learning (Translated in Chinese: exacity/deeplearningbook-chinese)

Update:

• 2017-02-12 Overview Update

• 2017-03-01 Update k-Nearest Neighbors

• 2017-03-08 Update SVM

• 2018-01-04 Update of fundamental knowledge of machine learning and mathematical knowledge in the book "Deep Learning"

• 2018-08-09 The content of Statistical Learning Methods has been posted in another article titled "Handwritten Notes on Statistical Learning Methods," and it is estimated that it will not be updated anymore. Later, some remaining contents in "Deep Learning" may be updated

i0H2cV.png

切换中文

Introduction to Statistical Learning Methods

Statistical Learning, Supervised Learning, Three Elements

• If a system can improve its performance by executing a certain process, that is learning

• The methods of statistical learning are based on constructing statistical models from data for the purpose of prediction and analysis

• Obtain the training dataset; determine the hypothesis space containing all possible models; establish the criteria for model selection; implement the algorithm for solving the optimal model; select the optimal model through learning methods; use the optimal model for predicting or analyzing new data

• The task of supervised learning is to learn a model that can make a good prediction for the corresponding output of any given input

• Each specific input is an instance, typically represented by a feature vector. It constitutes a feature space, with each dimension corresponding to a feature.

• Supervised learning learns a model from a training dataset, which consists of input-output pairs (samples)

• Supervised learning learns a model from a training set, represented as a conditional probability distribution or a decision function

• Statistical Learning Three Elements: Method = Model + Strategy + Algorithm. The model includes probabilistic models (conditional probability) and non-probabilistic models (decision functions); the strategy refers to the method of selecting the optimal model, introducing the concepts of loss function (cost function) and risk function, and realizing the optimization of empirical risk or structural risk; the algorithm refers to the specific computational method for learning the model.

• Loss function is used to measure the degree of error between the predicted values and the true values, common ones include: 0-1 loss function, squared loss function, absolute loss function, logarithmic loss function, denoted as \(L(Y,P(Y|X))\) , risk function (expected loss) is the average loss below the joint distribution of the model: \[ R_{exp}(f)=E_p[L(Y,f(X))]=\int_{x*y}L(y,f(x))P(x,y)dxdy \] , empirical risk (empirical loss) is the average loss of the model about the training set: \[ R_{emp}(f)=\frac 1N \sum_{i=1}^NL(y_i,f(x_i)) \]

• Ideally, expected risk can be estimated using empirical risk, however, when the sample size is small, minimizing empirical risk is prone to overfitting, thus the concept of structural risk (regularization) is proposed: \[ R_{srm}(f)=\frac1N \sum_{i=1}^NL(y_i,f(x_i))+ \lambda J(f) \] , where J(f) represents the complexity of the model, and the coefficient \(\lambda\) is used to weigh the empirical risk and model complexity. ML belongs to empirical risk minimization, while MAP belongs to structural risk minimization.

Model evaluation, model selection

• The error of the model on the training set and the test set is respectively called training error and test error. The loss function used may not be consistent, and making them consistent is ideal
• Overfitting: Learning too much, the complexity of the model is higher than the real model, performing well on the learned data but poor in predicting unknown data. To avoid overfitting, the correct number of features and the correct feature vectors are required.
• Two methods for model selection: regularization and cross-validation

Regularization, cross-validation

• Add a regularization term (penalty) to the empirical risk, with higher penalties for more complex models
• The general method is to randomly divide the dataset into three parts: the training set, the validation set, and the test set, which are used respectively for training data, selecting models, and finally evaluating the learning method. Cross-validation involves repeatedly randomly splitting the data into training and test sets, learning multiple times, and conducting testing and model selection.
• Cross-validation types: Simple cross-validation; S-fold cross-validation; Leave-one-out cross-validation

Generalization ability

• Generalization error: Error in predicting unknown data
• Generalization error upper bound is generally a function of the sample size; as the sample size increases, the upper bound of generalization tends to 0. This implies that the larger the hypothesis space capacity, the harder the model is to learn, and the larger the upper bound of the generalization error
• For binary classification problems, the upper bound of generalization error: where d is the capacity of the function set, for any function, at least with probability \(1-\delta\)

\[ R_{exp}(f)\leq R_{emp}(f)+\varepsilon (d,N,\delta ) \\ \varepsilon (d,N,\delta )=\sqrt{\frac 1{2N}(log d+log \frac 1 \delta)} \\ \]

Generative model, discriminative model

• The generation method is based on learning the joint probability distribution of data, and then calculating the conditional probability distribution as the predictive model, i.e., the generative model, such as the Naive Bayes method and the Hidden Markov Model
• Discriminant methods learn decision functions or conditional probability distributions directly from data as predictive models, i.e., discriminant models, such as k-nearest neighbors, perceptrons, decision trees, logistic regression models, maximum entropy models, support vector machines, boosting methods, and conditional random fields, etc
• The generation method can recover the joint probability distribution, has a fast learning convergence speed, and is suitable for cases with latent variables
• High accuracy of discrimination methods, capable of abstracting data, and simplifying learning problems

Categorization, annotation, regression

• Categorization, which takes discrete finite values as output, is also known as a classification decision function or classifier

• For binary classification, the total number of four cases: correctly predicted as correct TP; correctly predicted as incorrect FN; incorrectly predicted as correct FP; incorrectly predicted as incorrect TN

  \[ Precision:P=\frac{TP}{TP+FP} \\ Recall:R=\frac{TP}{TP+FN} \\ F1 value:\frac {2}{F_1}=\frac1P+\frac1R \\ \]

• Annotation: Input an observation sequence, output a marked sequence

• Regression: Function fitting, the commonly used loss function is the squared loss function, which is fitted using the least squares method

k-Nearest Neighbors method

k-Nearest Neighbors method

• k-Nearest Neighbor method assumes that a training dataset is given, with instances of predetermined categories. In classification, for new instances, predictions are made based on the categories of the k nearest training instances, through majority voting or other methods.
• k-value selection, distance measurement, and classification decision rules are the three elements of the k-nearest neighbor method.
• k-Nearest Neighbor is a lazy learning method; it does not train the samples.

k-Nearest Neighbors algorithm

• For new input instances, find the k nearest instances to the instance in the training dataset, and if the majority of these k instances belong to a certain class, classify the instance into that class. That is:

  \[ y=arg \max_{c_j} \sum_{x_i \in N_k(x)} I(y_i=c_j), \ i=1,2,...,N; \ j=1,2,...,K \]

  When \(y_i=c_i\) is \(I=1\) , the neighborhood \(N_k(x)\) consists of k nearest neighbor points covering x.

• When k=1, it is called the nearest neighbor algorithm

• k-nearest neighbor algorithm does not have an explicit learning process

k-Nearest Neighbors model

• k-nearest neighbor model refers to the partitioning of the feature space.

• In the feature space, for each training instance point, all points closer to this point than others form a region called a unit. Each training instance point has a unit, and the units of all training instance points constitute a partition of the feature space, with the class of each instance being the class label of all points within its unit.

• Distance metrics include: Euclidean distance, \(L_p\) distance, Minkowski distance.

• The Euclidean distance is a special case of the \(L_p\) distance (p=2), and when p=1, it becomes the Manhattan distance, defined as:

  \[ L_p(x_i,x_j)=(\sum _{l=1}^n |x_i^{(l)}-x_j^{(l)}|^p)^{\frac1p} \]

• k value is small, approximation error is small, estimation error is large, the overall model is complex, prone to overfitting. k value is large, estimation error is small, approximation error is large, the model is simple

• Generally, the cross-validation method is used to determine the value of k

• The majority voting rule is equivalent to empirical risk minimization

k-d tree

• kd-tree is a special structure used to store training data, which improves the efficiency of k-nearest neighbor search, which is essentially a binary search tree
• Each node of the k-d tree corresponds to a k-dimensional hyperrectangle region
• Method for constructing a balanced kd-tree: Divide by taking the median of each dimension sequentially, for example, in three dimensions, first draw a line at the median of the x-axis, divide it into two parts, then draw a line at the median of the y-axis for each part, and then along the z-axis, and then cycle through x, y, z.
• After the construction of the kd-tree is completed, it can be used for k-nearest neighbor searches. The following uses the nearest neighbor search as an example, where k=1:
  • Starting from the root node, recursively search downwards to the area where the target point is located, until reaching the leaf nodes
  • Taking this leaf node as the current nearest point, the distance from the current nearest point to the target point is the current nearest distance, and our goal is to search the tree to find a suitable node to update the current nearest point and the current nearest distance
  • Recursive upward rollback, perform the following operation on each node
    • If the instance point saved by the node is closer to the target point than the current nearest point, update the instance point to the current nearest point, and update the distance from the instance point to the target point to the current nearest distance
    • The child nodes of this node are divided into two, one of which contains our target point. This part we have come from the target point all the way up recursively, and it has been updated. Therefore, we need to find the other child node of this node to see if it can be updated: Check if the corresponding area of the other child node intersects with the hypersphere centered at the target point and with the current shortest distance as the radius. If they intersect, move to this child node and continue the upward search; if they do not intersect, do not move and continue the upward search.
    • Until the root node is searched, the current nearest point at this time is the nearest neighbor of the target point.
• The computational complexity of k-d tree search is \(O(logN)\) , suitable for k-nearest neighbor search when the number of training instances is much larger than the number of spatial dimensions

Support Vector Machine

Linearly separable support vector machine and hard margin maximization

• The goal of learning is to find a separating hyperplane in the feature space that can distribute instances into different classes (binary classification). The separating hyperplane corresponds to the equation \(wx+b=0\) , determined by the normal vector w and the intercept b, and can be represented by (w, b)

• Here, x is the feature vector \((x_1,x_2,...)\) , and y is the label of the feature vector

• Given a linearly separable training dataset, the separating hyperplane learned by maximizing the margin or solving the equivalent convex quadratic programming problem, denoted as \(wx+b=0\) , and the corresponding classification decision function denoted as \(f(x)=sign(wx+b)\) , is called a linearly separable support vector machine

• Under the determination of the hyperplane \(wx+b=0\) , the distance from the point (x,y) to the hyperplane can be

  \[ \gamma _i=\frac{w}{||w||}x_i+\frac{b}{||w||} \]

• Whether the symbol of \(wx+b\) is consistent with the symbol of class label y indicates whether the classification is correct, \(y=\pm 1\) , thus obtaining the geometric distance

  \[ \gamma _i=y_i(\frac{w}{||w||}x_i+\frac{b}{||w||}) \\ Define the geometric interval of the hyperplane (w,b) with respect to the training data set T as the minimum geometric interval of all sample points \\ \gamma=min\gamma _i \\ \]

• Simultaneously define the relative distance as the function interval

  \[ \gamma _i=y_i(wx_i+b) \\ \gamma =min\gamma _i \\ \]

• Hard margin maximization is for linearly separable hyperplanes, while soft margin maximization is for approximately linearly separable cases

• Finding a hyperplane with the maximum geometric margin, which can be represented as the following constrained optimization problem

  \[ max_{(w,b)} \gamma \\ s.t. \quad y_i(\frac{w}{||w||}x_i+\frac{b}{||w||})\geq \gamma ,i=1,2,...,N \\ \]

• We can convert geometric intervals into functional intervals, which has no effect on optimization. Moreover, if we fix the relative interval as a constant (1), the maximization of the geometric interval can be transformed into the minimization of \(||w||\) , thus the constrained optimization problem can be rewritten as

  \[ min_{(w,b)} \frac12 {||w||}^2 \\ s.t. \quad y_i(wx_i+b)-1 \geq 0 \\ \]

• The above equation is the basic form of SVM, and when the above optimization problem is solved, we obtain a separating hyperplane with the maximum margin, which is the maximum margin method

• The maximum margin separating hyperplane exists and is unique, proof omitted

• In the linearly separable case, the instances of the nearest sample points to the separating hyperplane in the training dataset are called support vectors

• For the positive example points of \(y_i=1\) , the support vectors lie on the plane \(wx+b=1\) , similarly, the negative example points lie on the plane \(wx+b=-1\) . These two planes are parallel and there are no training data points between them. The distance between the two planes is the margin, which depends on the normal vector w of the separating hyperplane, as \(\frac 2 {||w||}\)

• Thus, it can be seen that support vector machines are determined by a very small number of important training samples (support vectors)

• To solve the optimization problem, we introduce the dual algorithm and also introduce kernel functions to generalize to nonlinear classification problems

• To be supplemented

Linear Algebra Basics

Moore-penrose

• For non-square matrices, their inverse matrix is undefined, therefore we specially define the pseudoinverse of non-square matrices: Moore-Penrose pseudoinverse \[ A^+=lim_{\alpha \rightarrow 0}(A^TA+\alpha I)^{-1}A^T \]

• The actual algorithms for computing the pseudo-inverse do not base themselves on this definition, but rather use the following formula:

  \[ A^+=VD^+U^T \]

  U, D, and V are the matrices obtained from the singular value decomposition of matrix A, which are diagonal matrices. The pseudo-inverse \(D^+\) of the diagonal matrix D is obtained by taking the reciprocal of its non-zero elements and then transposing.

• When the number of columns of matrix A exceeds the number of rows, using the pseudoinverse to solve the linear equation is one of many possible methods. Particularly, \(x = A^+y\) is the one with the smallest Euclidean norm among all feasible solutions to the equation.

• When the number of rows of matrix A exceeds the number of columns, there may be no solution. In this case, the pseudo-inverse \(x\) obtained minimizes the Euclidean distance between \(Ax\) and \(y\) .

• To be supplemented

迹

• Trace operation returns the sum of the diagonal elements of the matrix.

• Using trace operations, the matrix Frobenius norm can be described as:

  \[ ||A_F||=\sqrt{Tr(AA^T)} \]

• Trace has transposition invariance and permutation invariance

• The trace of a scalar is its own

PCA Explanation

• To be supplemented

Probability Theory and Information Theory

Logistic Sigmoid

• Logistic and sigmoid are often used interchangeably, this function is used to compress real numbers into the interval (0,1), representing binary classification probabilities:

  \[ \sigma (x) = \frac{1}{1+exp(-x)} \]

• Softmax is an extension of the sigmoid, being a smoothed version of the argmax function (argmax returns a one-hot vector while softmax returns probabilities for various possible outcomes), extending binary classification to the multi-class (disjoint) case:

  \[ \sigma (z)_j = \frac{e^z j}{\sum _{k=1}^K e^z k} \]

• Both exhibit saturation phenomena when the input is too large or too small, but when the two functions are introduced as nonlinear activation units in a neural network, because the cost function takes the negative logarithm, this saturation phenomenon can be eliminated.

• Softmax function, due to the inclusion of exponential functions, also has issues with underflow and overflow. When the input is uniformly distributed and the number of input samples is large, the denominator exponential values approach 0, and the summation may also approach 0, leading to underflow in the denominator. Overflow can also occur when the parameters of the exponential function are large. The solution is to process the input x as z = x - max(xi), that is, subtracting the maximum component from each component of the vector. Adding or subtracting a scalar from the input vector does not change the softmax function values (redundancy of the softmax function), but at this point, the maximum value of the processed input is 0, excluding overflow. After the exponential function, at least one term in the summation of the denominator exists as 1, excluding underflow.

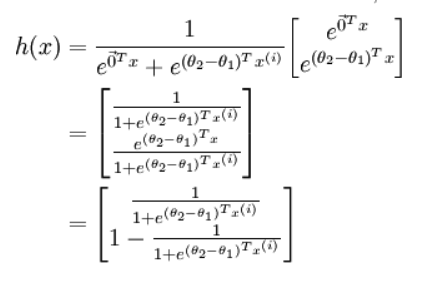
• Utilizing the redundancy of the softmax function can also deduce that sigmoid is a special case of softmax:

KL divergence and cross-entropy

• KL divergence: A measure of the difference between two distributions, PQ, non-negative and asymmetric:

  \[ D_{KL}(P||Q) = E_{x \sim P} [log \frac{P(x)}{Q(x)}] = E_{x \sim P} [log P(x) - log Q(x)] \]

• Cross-entropy:

  \[ H(P,Q) = -E_{x \sim P} log Q(x) \]

• The cross-entropy form is simple, and the minimization of KL divergence with respect to Q (actual output) is unrelated to the first term in the divergence formula, therefore, minimizing KL divergence can actually be seen as minimizing cross-entropy. Moreover, since KL divergence represents the difference between PQ (actual output and correct output), it can be regarded as a loss function

• In dealing with binary classification problems using logistic regression, q(x) refers to the logistic function, and p(x) refers to the actual distribution of the data (either 0 or 1)

• The expected self-information of q with respect to p, i.e., the binary cross-entropy (Logistic cost function):

  \[ J(\theta) = - \frac 1m [\sum _{i=1}^m y^{(i)} log h_{\theta} (x^{(i)}) + (1-y^{(i)}) log (1-h_{\theta}(x^{(i)}))] \]

• Similarly, we can obtain the multi-class cross-entropy (Softmax cost function):

  \[ J(\theta) = - \frac 1m [\sum _{i=1}^m \sum _{j=1}^k 1\{ y^{(i)}=j \} log \frac {e^{\theta _j ^T x^{(i)}}} {\sum _{l=1}^k e^{\theta _j ^T x^{(i)}}}] \]

Cross-entropy and maximum log-likelihood relationship

• Given a sample dataset X with distribution \(P_{data}(x)\) , we aim to obtain a model \(P_{model}(x,\theta)\) whose distribution is as close as possible to \(P_{data}(x)\) . \(P_{model}(x,\theta)\) maps any x to a real number to estimate the true probability \(P_{data}(x)\) . In \(P_{model}(x,\theta)\) , the maximum likelihood estimate of \(\theta\) is the \(\theta\) that maximizes the product of probabilities obtained by the model for the sample data:

  \[ \theta _{ML} = \mathop{argmax}\limits_{\theta} p_{model} (X;\theta) \]

• Because taking the logarithm and scaling transformation does not change argmax, taking the logarithm transforms it into a summation and then dividing by the sample size to average it yields:

  \[ \theta _{ML} = \mathop{argmax}\limits_{\theta} E_{x \sim p_{data}} log p_{model}(x;\theta) \]

• It can be observed that the above expression is the negative of the cross-entropy, and its value is maximized when Pdata(x) = Pmodel(x,θ), so:

• Maximum likelihood = minimum negative log-likelihood = minimizing cross-entropy = minimizing KL divergence = minimizing the gap between data and model = minimizing the cost function

• Maximum likelihood estimation can be extended to maximum conditional likelihood estimation, which constitutes the foundation of most supervised learning: Formula:

  \[ \theta _{ML} = \mathop{argmax}\limits_{\theta} \sum_{i=1}^m log P(y^{(i)} | x^{(i)} ; \theta) \]

• Maximum likelihood estimation is consistent.

Computational Method

Gradient Descent

• How to transform parameters (inputs) to make the function smaller (minimize the cost function)?
• The principle is that moving the input in the opposite direction of the derivative by a small step can reduce the function's output.
• Extend the input to vector-form parameters, treat the function as a cost function, and thus obtain a gradient-based optimization algorithm.
• First-order optimization algorithm: including gradient descent, using the Jacobian matrix (including the relationship between partial derivatives of vectors), and updating the suggested parameter updates through gradient descent:

Newton's Method

• Second-order optimization algorithm (求最优补偿，定性临界点): First-order optimization requires adjusting the appropriate learning rate (step size), otherwise it cannot reach the optimal point or will produce shaking, and it cannot update the parameters at the critical point (gradient is 0), which reflects the need for second-order derivative information of the cost function, for example, when the function is convex or concave, the predicted value based on the gradient and the true value of the cost function have a deviation. The Hessian matrix contains second-order information. Newton's method uses the information of the Hessian matrix, uses the second-order Taylor expansion to obtain the function information, and updates the parameters using the following formula:  

Constraint Optimization

• Only contains equality constraint conditions: Lagrange

• Inequality constraint conditions: KTT

Modify algorithm

Modify the hypothesis space

• Machine learning algorithms should avoid overfitting and underfitting, which can be addressed by adjusting the model capacity (the ability to fit various functions).

• Adjusting the model capacity involves selecting an appropriate hypothesis space (assuming input rather than parameters), for example, previously only fitting polynomial linear functions:

  \[ y = b + wx \]

• If nonlinear units, such as higher-order terms, are introduced, the output remains linearly distributed relative to the parameters:

  \[ y= b + w_1 x + w_2 x^2 \]

  This increases the model's capacity while simplifying the generated parameters, making it suitable for solving complex problems; however, a too high capacity may also lead to overfitting.

Regularization

• No free lunch theorem (after averaging over all possible data generation distributions, each classification algorithm has the same error rate on points that have not been observed beforehand) indicates that machine learning algorithms should be designed for specific tasks, and algorithms should have preferences. Adding regularization to the cost function introduces preferences, causing the learned parameters to be biased towards minimizing the regularization term.

• An example is weight decay; the cost function with the addition of the weight decay regularization term is:

  \[ J(w) = MSE_{train} + \lambda w^T w \]

  λ controls the preference degree, and the generated models tend to have small parameters, which can avoid overfitting.

统计学习方法概论

统计学习，监督学习，三要素

• 如果一个系统能够通过执行某个过程改进它的性能，这就是学习
• 统计学习的方法是基于数据构建统计模型从而对数据进行预测和分析
• 得到训练数据集合；确定包含所有可能模型的假设空间；确定模型选择的准则；实现求解最优模型的算法；通过学习方法选择最优模型；利用最优模型对新数据进行预测或分析
• 监督学习的任务是学习一个模型，是模型对任意给定的输入，对其相应的输出做出一个好的预测
• 每个具体的输入是一个实例，通常由特征向量表示。构成特征空间，每一维对应一个特征
• 监督学习从训练数据集合中学习模型，训练数据由输入与输出对构成(样本)
• 监督学习从训练集中学习到一个模型，表示为条件概率分布或者决策函数
• 统计学习三要素:方法=模型+策略+算法。模型包括概率模型(条件概率)和非概率模型(决策函数)；策略即选择最优模型的方法，引入损失函数(代价函数)，风险函数的概念，实现经验风险或者结构风险最优化；算法是指学习模型的具体计算方法
• 损失函数用来度量预测值相比真实值的错误程度，常见的有:0-1损失函数，平方损失函数，绝对损失函数对数损失函数，记为\(L(Y,P(Y|X))\),风险函数(期望损失)是模型在联合分布的平均以下的损失：\[R_{exp}(f)=E_p[L(Y,f(X))]=\int_{x*y}L(y,f(x))P(x,y)dxdy\]经验风险(经验损失)是模型关于训练集的平均损失:\[R_{emp}(f)=\frac 1N \sum_{i=1}^NL(y_i,f(x_i))\]
• 理想情况下，可以用经验风险估计期望风险，然而样本容量很小时，经验风险最小化易导致过拟合，从而提出了结构风险(正则化)：\[R_{srm}(f)=\frac1N \sum_{i=1}^NL(y_i,f(x_i))+ \lambda J(f)\],其中J(f)为模型的复杂性，系数\(\lambda\)用来权衡经验风险和模型复杂度。ML属于经验风险最小化，MAP属于结构风险最小化

模型评估，模型选择

• 模型在训练集和测试集上的误差分别称为训练误差和测试误差，所用的损失函数不一定一致，让两者一致是比较理想的
• 过拟合:学过头了，模型的复杂度比真实模型要高，只对学过的数据性能良好，对未知数据的预测能力差。避免过拟合需要正确的特征个数和正确的特征向量
• 模型选择的两种方法：正则化和交叉验证

正则化，交叉验证

• 即在经验风险上加一个正则化项(罚项)，模型越复杂惩罚越高
• 一般方法是将数据集随机的分成三部分:训练集、验证集、测试集，分别用来训练数据，选择模型，最终对学习方法的评估。交叉验证是将数据反复随机切分为训练集和测试集，学习多次，进行测试和模型选择
• 交叉验证类型:简单交叉验证;S折交叉验证;留一交叉验证

泛化能力

• 泛化误差:对未知数据预测的误差
• 泛化误差上界，一般是样本容量的函数，当样本容量增加时，泛化上界趋于0，是假设空间容量越大，模型就越难学，泛化误差上界就越大
• 对于二分类问题，泛化误差上界：其中d是函数集合容量，对任意一个函数，至少以概率\(1-\delta\)

\[ R_{exp}(f)\leq R_{emp}(f)+\varepsilon (d,N,\delta ) \\ \varepsilon (d,N,\delta )=\sqrt{\frac 1{2N}(log d+log \frac 1 \delta)} \\ \]

生成模型，判别模型

• 生成方法由数据学习联合概率分布，然后求出条件概率分布作为预测的模型，即生成模型，比如朴素贝叶斯法和隐马尔科夫模型
• 判别方法由数据直接学习决策函数或者条件概率分布作为预测的模型，即判别模型，比如k近邻法、感知机、决策树、逻辑斯蒂回归模型、最大熵模型、支持向量机、提升方法和条件随机场等
• 生成方法可以还原联合概率分布，学习收敛速度快，适用于存在隐变量的情况
• 判别方法准确率高，可以抽象数据，简化学习问题

分类，标注，回归

• 分类，即输出取离散有限值，分类决策函数也叫分类器

• 对于二分类，四种情况的总数:对的预测成对的TP;对的预测成错的FN；错的预测成对的FP；错的预测成错的TN

  \[ 精确率:P=\frac{TP}{TP+FP} \\ 召回率:R=\frac{TP}{TP+FN} \\ 1F值:\frac {2}{F_1}=\frac1P+\frac1R \\ \]

• 标注:输入一个观测序列，输出一个标记序列

• 回归：函数拟合，常用的损失函数是平方损失函数，利用最小二乘法拟合

k近邻法

k近邻法

• k近邻法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其k个最近邻的训练实例的类别，通过多数表决等方式进行预测。
• k值选择，距离度量以及分类决策规则是k近邻法三要素。
• k近邻法是一种懒惰学习，他不对样本进行训练。

k近邻算法

• 对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把该实例分到这个类。即:

  \[ y=arg \max_{c_j} \sum_{x_i \in N_k(x)} I(y_i=c_j), \ i=1,2,...,N; \ j=1,2,...,K \]

  其中\(y_i=c_i\)时\(I=1\)，\(N_k(x)\)是覆盖x的k个近邻点的邻域。

• k=1时称为最近邻算法

• k近邻算法没有显式的学习过程

k近邻模型

• k近邻模型即对特征空间的划分。

• 特征空间中，对于每个训练实例点，距离该点比其他点更近的所有点组成一个区域，叫做单元。每一个训练实例点拥有一个单元，所有训练实例点的单元构成对特征空间的一个划分，每个实例的类是其单元中所有点的类标记。

• 距离度量包括：欧氏距离，\(L_p\)距离，Minkowski距离。

• 欧氏距离是\(L_p\)距离的一种特殊情况(p=2)，p=1时即曼哈顿距离，定义为：

  \[ L_p(x_i,x_j)=(\sum _{l=1}^n |x_i^{(l)}-x_j^{(l)}|^p)^{\frac1p} \]

• k值较小，近似误差小，估计误差大，整体模型复杂，容易发生过拟合。k值较大，估计误差小，近似误差大，模型简单

• 一般采用交叉验证法确定k值

• 多数表决规则等价于经验风险最小化

kd树

• kd树是用来存储训练数据的特殊结构，提高了k近邻搜索的效率，其实就是一种二叉查找树
• kd树的每一个节点对应于一个k维超矩形区域
• 构造平衡kd树的方法:依次对各个维度上取中位数进行划分，例如三维，先以x轴上中位数划线，分为两部分，每一个部分在以y轴中位数划线，然后再z轴，然后再x,y,z循环。
• 构造完成kd树后就可以利用kd树进行k近邻搜索，以下用最近邻搜索为例，即k=1：
  • 从根节点出发，递归向下搜索目标点所在区域，直到叶节点
  • 以此叶节点为当前最近点，当前最近点到目标点的距离是当前最近距离，我们的目标就是在树中搜索，找到合适的节点更新当前最近点和当前最近距离
  • 递归向上回退，对每个节点做如下操作
    • 如果该节点保存的实例点比当前最近点距离目标点更近，则更新该实例点为当前最近点，更新该实例点到目标点的距离为当前最近距离
    • 该节点的子节点分为两个，其中一个包含了我们的目标点，这一部分我们是从目标点一路向上递归过来的，已经更新完了，因此要找该节点的另外一个子节点，看看可不可以更新：检查另一子节点对应区域是否与以目标点为球心，当前最近距离为半径的超球体相交，相交的话就移动到这个子节点，然后接着向上搜索，不相交则不移动，依然接着向上搜索。
    • 直到搜索到根节点，此时的当前最近点即目标点的最近邻点。
• kd树搜索的计算复杂度是\(O(logN)\)，适用于训练实例数远大于空间维数的k近邻搜索

支持向量机

线性可分支持向量机与硬间隔最大化

• 学习的目标是在特征空间中找到一个分离超平面，能将实例分到不同的类(二分类)，分离超平面对应于方程\(wx+b=0\)，由法向量w和截距b决定，可由(w,b)表示

• 这里的x是特征向量\((x_1,x_2,...)\)，而y是特征向量的标签

• 给定线性可分训练数据集，通过间隔最大化或者等价的求解相应的凸二次规划问题学习得到的分离超平面为\(wx+b=0\)，以及相应的分类决策函数\(f(x)=sign(wx+b)\)称为线性可分支持向量机

• 在超平面\(wx+b=0\)确定的情况下，点(x,y)到超平面的距离可以为

  \[ \gamma _i=\frac{w}{||w||}x_i+\frac{b}{||w||} \]

• 而\(wx+b\)的符号与类标记y的符号是否一致可以表示分类是否正确，\(y=\pm 1\)，这样就可以得到几何间隔

  \[ \gamma _i=y_i(\frac{w}{||w||}x_i+\frac{b}{||w||}) \\ 定义超平面(w,b)关于训练数据集T的几何间隔为关于所有样本点的几何间隔的最小值 \\ \gamma=min\gamma _i \\ \]

• 同时定义相对距离为函数间隔

  \[ \gamma _i=y_i(wx_i+b) \\ \gamma =min\gamma _i \\ \]

• 硬间隔最大化针对线性可分超平面而言，软间隔最大化针对近似线性可分而言

• 求一个几何间隔最大的分离超平面，可以表示为下面的约束最优化问题

  \[ max_{(w,b)} \gamma \\ s.t. \quad y_i(\frac{w}{||w||}x_i+\frac{b}{||w||})\geq \gamma ,i=1,2,...,N \\ \]

• 我们可以将几何间隔转化为函数间隔，对最优化没有影响，同时，如果我们固定相对间隔为常量(1)，则对几何间隔的最大化可以转化为对\(||w||\)的最小化，因此约束最优化问题可以改写为

  \[ min_{(w,b)} \frac12 {||w||}^2 \\ s.t. \quad y_i(wx_i+b)-1 \geq 0 \\ \]

• 上式就是SVM的基本型,当解出以上最优化问题时，我们就得到了一个拥有最大间隔的分离超平面，这就是最大间隔法

• 最大间隔分离超平面存在且唯一，证明略

• 在线性可分情况下，训练数据集的样本点中分离超平面最近的样本点的实例称为支持向量

• 对\(y_i=1\)的正例点，支持向量在平面\(wx+b=1\)上，同理负例点在平面\(wx+b=-1\)上，这两个平面平行，之间没有任何训练数据点，两个平面的间隔距离为间隔(margin)，间隔依赖于分离超平面的法向量w，为\(\frac 2 {||w||}\)

• 由此可见支持向量机由很少的重要的训练样本(支持向量)决定

• 为了解最优化问题，我们引入对偶算法，同时引入核函数以便推广到非线性分类问题

• 待补充

线代基础

Moore-penrose

• 对于非方矩阵，其逆矩阵没有定义，因此我们特别定义非方矩阵的伪逆：Moore-Penrose 伪逆 \[ A^+=lim_{\alpha \rightarrow 0}(A^TA+\alpha I)^{-1}A^T \]

• 计算伪逆的实际算法没有基于这个定义，而是使用下面的公式：

  \[ A^+=VD^+U^T \]

  其中U、D、V是矩阵A奇异值分解后得到的矩阵，对角矩阵。对角矩阵 D 的伪逆\(D^+\)是其非零元素取倒数之后再转置得到的。

• 当矩阵 A 的列数多于行数时，使用伪逆求解线性方程是众多可能解法中的一种。特别地，\(x = A^+y\)是方程所有可行解中欧几里得范数最小的一个。

• 当矩阵 A 的行数多于列数时，可能没有解。在这种情况下，通过伪逆得到的\(x\)使得\(Ax\)和\(y\)的欧几里得距离最小。

• 待补充

迹

• 迹运算返回的是矩阵对角元素的和.

• 使用迹运算可以描述矩阵Frobenius范数的方式：

  \[ ||A_F||=\sqrt{Tr(AA^T)} \]

• 迹具有转置不变性和轮换不变性

• 标量的迹是其本身

PCA解释

• 待补充

概率论信息论

Logistic Sigmoid

• Logistic和sigmoid两种称呼经常混用，这个函数用于将实数压缩到(0,1)之间，代表二分类概率：

  \[ \sigma (x) = \frac{1}{1+exp(-x)} \]

• Softmax 是sigmoid的扩展版，是argmax函数的软化版本（argmax返回一个one hot 向量而softmax返回的是各种可能的概率），将二分类扩展到多分类（互斥）情况：

  \[ \sigma (z)_j = \frac{e^z j}{\sum _{k=1}^K e^z k} \]

• 两者在输入过大过小时都存在饱和现象，但将两个函数作为非线性激活单元引入神经网络时，因为代价函数是取负对数，可以消除这种饱和现象。

• Softmax函数因为包含指数函数，还存在上下溢出问题。当输入均匀分布且输入样本数量很大时，分母指数值接近于0，累加也可能接近于0，导致分母下溢。当指数函数参数很大时也会导致上溢。解决办法是将输入x处理为z=x-max(xi)，即向量的每个分量都减去最大分量，输入向量加减标量不会导致softmax函数值改变(softmax函数的冗余性），但此时输入经处理后最大值为0，排除上溢，经过指数函数后分母的累加项中至少存在一个1，排除下溢。

• 利用softmax函数的冗余性也可以推出sigmoid是softmax的一种特例：

KL散度和交叉熵

• KL散度：用以衡量PQ两个分布之间的差异，非负且不对称：

  \[ D_{KL}(P||Q) = E_{x \sim P} [log \frac{P(x)}{Q(x)}] = E_{x \sim P} [log P(x) - log Q(x)] \]

• 交叉熵：

  \[ H(P,Q) = -E_{x \sim P} log Q(x) \]

• 交叉熵形式简单，而且针对Q（实际输出）最小化KL散度与散度公式中前一项无关系，因此最小化KL散度实际上可以看成最小化交叉熵，又因为KL散度代表PQ（实际输出和正确输出）之间的差异，即可以看作是损失函数

• 在用logistic处理二分类问题中，q(x)即logistic函数,p(x)即实际数据的正确分布(0或者1)

• 对q按照p求自信息期望即二元交叉熵(Logistic代价函数):

  \[ J(\theta) = - \frac 1m [\sum _{i=1}^m y^{(i)} log h_{\theta} (x^{(i)}) + (1-y^{(i)}) log (1-h_{\theta}(x^{(i)}))] \]

• 同理可得多元交叉熵(Softmaxs代价函数):

  \[ J(\theta) = - \frac 1m [\sum _{i=1}^m \sum _{j=1}^k 1\{ y^{(i)}=j \} log \frac {e^{\theta _j ^T x^{(i)}}} {\sum _{l=1}^k e^{\theta _j ^T x^{(i)}}}] \]

交叉熵与最大对数似然关系

• 已知一个样本数据集X，分布为\(P_{data}(x)\)，我们希望得到一个模型\(P_{model}(x,\theta)\)，其分布尽可能接近\(P_{data}(x)\)。\(P_{model}(x,\theta)\)将任意x映射为实数来估计真实概率\(P_{data}(x)\)。 在\(P_{model}(x,\theta)\)中，对\(\theta\)的最大似然估计为使样本数据通过模型得到概率之积最大的\(\theta\)：

  \[ \theta _{ML} = \mathop{argmax}\limits_{\theta} p_{model} (X;\theta) \]

• 因为取对数和尺度变换不会改变argmax，取对数变累加并除以样本数量平均后得到：

  \[ \theta _{ML} = \mathop{argmax}\limits_{\theta} E_{x \sim p_{data}} log p_{model}(x;\theta) \]

• 可以发现上式即交叉熵的相反数，当Pdata(x)=Pmodel(x,θ)时上式值最大，所以:

• 最大似然=最小负对数似然=最小化交叉熵=最小化KL散度=最小化数据与模型之间的差距∈最小化代价函数

• 最大似然估计可扩展到最大条件似然估计，构成了大多数监督学习基础：公式：

  \[ \theta _{ML} = \mathop{argmax}\limits_{\theta} \sum_{i=1}^m log P(y^{(i)} | x^{(i)} ; \theta) \]

• 最大似然估计具有一致性。

计算方法

梯度下降

• 问题：为了使函数变小（最小化代价函数），怎样变换参数（输入）？
• 原理：将输入向导数的反方向移动一小步可以减小函数输出。
• 将输入扩展到向量形式的参数，将函数看成代价函数，即得到基于梯度的优化算法。
• 一阶优化算法：包括梯度下降，使用Jacobian矩阵（包含向量之间偏导数关系），通过梯度下降对参数的建议更新为：

牛顿法

• 二阶优化算法：（求最优补偿，定性临界点）:一阶优化需要调整合适的学习率（步长），否则无法达到最优点或者会产生抖动，且在临界点（梯度为0）无法更新参数，这反映我们需要代价函数的二阶导数信息，例如函数向上凸出或向下凸出时基于梯度的预测值和真实的代价函数值之间有偏差。Hessian矩阵包含了二阶信息。牛顿法使用了Hessian矩阵的信息，利用泰勒二阶展开得到函数信息，利用下式更新参数：

  约束优化

• 只包含等式约束条件：Lagrange

• 包含不等式约束条件：KTT

修改算法

修改假设空间

• 机器学习算法应避免过拟合和欠拟合，可以通过调整模型容量（拟合各种函数的能力）来解决。

• 调整模型容量的方案是选择合适的假设空间（假设输入而不是参数），例如之前只拟合多项式线性函数：

  \[ y = b + wx \]

• 如果引入非线性单元，例如高次项，输出相对于参数仍然是线性分布：

  \[ y= b + w_1 x + w_2 x^2 \]

  此时就增加了模型的容量，但简化了生成的参数，适用于解决复杂的问题，然而容量太高也有可能过拟合。

正则化

• 没有免费午餐定理（在所有可能的数据生成分布上平均之后，每一个分类算法在未事先观测的点上都有相同的错误率）说明应在特定任务上设计机器学习算法，算法应该有偏好。将代价函数中加入正则化即引入偏好，使得学习到的参数偏向于使正则化项变小。

• 一个例子是权重衰减，加入权重衰减正则化项的代价函数是：

  \[ J(w) = MSE_{train} + \lambda w^T w \]

  λ控制偏好程度，生成的模型倾向于小参数，可以避免过拟合。