NLP Basics

Recorded some basic knowledge of deep learning learned when recording the seq2seq model in the entry-level NLP.

i0I5WV.jpg

切换中文

Neural Networks with Feedforward Architecture

• When the dimensionality of the data is very high, the capacity of the sample space may be much greater than the number of training samples, leading to the curse of dimensionality.

• Activation function. Used to represent the nonlinear transformation in neural networks. Without an activation function, if the neural network only has a weight matrix, it is a combination of linear transformations and remains a linear transformation. The use of nonlinear transformations can extract features that are convenient for linear transformations, avoiding the dimensionality disaster (?).

• Softmax and sigmoid significance: Maximum entropy, convenient for differentiation, universal approximation theorem (with squeezing property)

• Hidden layers can use the activation function ReLU, i.e., rectified linear, but the drawback is that it cannot use gradient learning to activate the function to 0 for the samples, so three extensions have been developed:

  \[ g(z,\alpha)_i = max(0,z_i) + \alpha _i min(0,z_i) \]

  Absolute value rectification: right coefficient is -1; leakage rectification: right coefficient is fixed to a smaller value; parameterized rectification: coefficients are placed in the model for learning

Backpropagation

• Backpropagation calculates the parameter update values by determining the output biases through gradients, updating parameters layer by layer from the output layer to the input layer, propagating the gradients used by the previous layer, and utilizing the chain rule of calculus for vectors. The update amount for each layer = the Jacobian matrix of the current layer * the gradient of the previous layer.
• Backpropagation in Neural Networks: Initialize the gradient table. The last layer's output calculates the gradient with respect to the output, so the initial value is 1. The loop proceeds from the end to the beginning, with the gradient table of the current layer being the product of the current layer's Jacobian matrix and the gradient table of the previous layer (i.e., chain rule differentiation). The current layer uses the gradient table of the previous layer for calculation and storage, avoiding repeated calculations in the chain rule.

Recurrent Neural Network (RNN)

Recurrent Neural Network

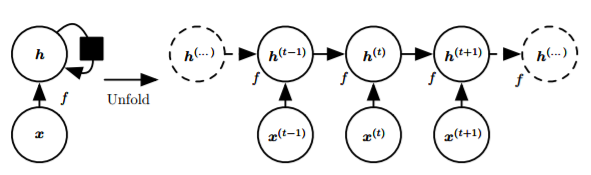
• Features: All hidden layers share parameters, treating hidden layers as state variables for convenient parameterization.

• Using hyperbolic tangent as the hidden layer activation function

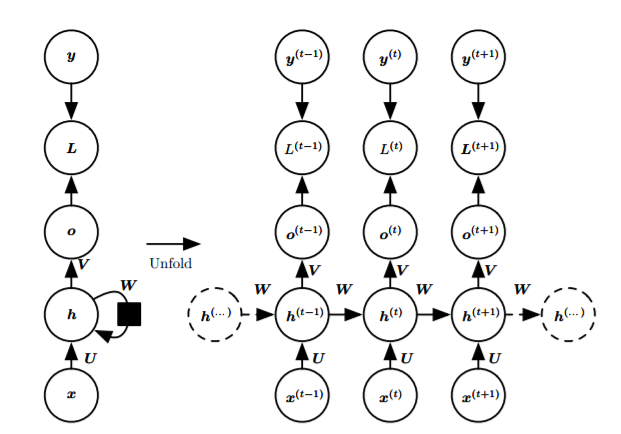
• Input x, x passes through a weighted matrix and is activated by a hidden layer to obtain h, h passes through a weighted matrix to output o, the cost L, and o is activated by an output layer to obtain y

• Basic Structure (Expanded and Non-Expanded):

• Several variants:

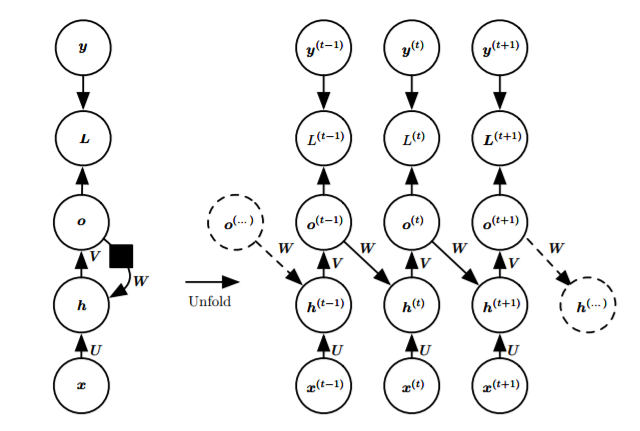
  • Each time step has an output, with recurrent connections between hidden layers:
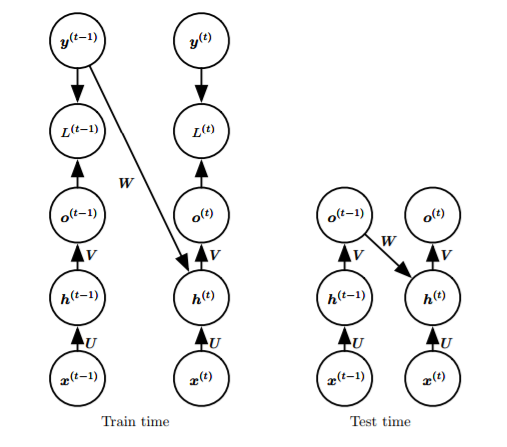
  • Each time step has an output, and there is a recurrent connection between the output and the hidden layer:
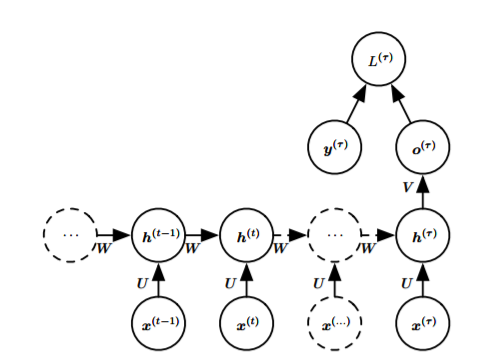
  • Read the entire sequence and produce a single output:

• Common forward propagation, softmax processing of output, negative log-likelihood as the loss function, and the cost of backpropagation through time is too high. Feedforward process:

  \[ \alpha ^{(t)} = b + Wh^{(t-1)} + Ux^{(t)}, \\ h^{(t)} = tanh(a^{(t)}), \\ o^{(t)} = c + Vh^{(t)}, \\ y^{(t)} = softmax(o^{(t)}) \\ \]

  Cost function:

  \[ L(\{ x^{(1)} , ... , x^{(\tau)}\},\{ y^{(1)} , ... , y^{(\tau)}\}) \\ =\sum _t L^{(t)} \\ = - \sum _t log p_{model} (y^{(t)}|\{ x^{(1)} , ... , x^{(\tau)}\}) \\ \]

• Replaced with the second RNN, using output-to-hidden layer loops, eliminating hidden-to-hidden layer loops, decoupling parallel(?), using a mentor-driven model (train the loop network W to the hidden layer with correct outputs, and use the actual output close to the correct output during testing) Mentor-driven model:

Bidirectional RNN

• Considering the dependency on future information, it is equivalent to the combination of two hidden layers

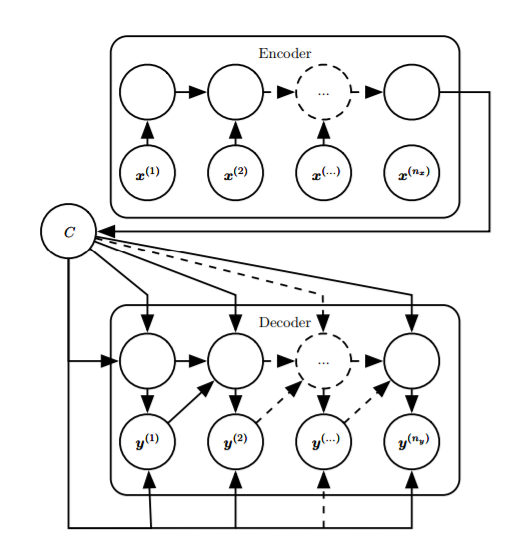
Sequence to sequence

• Using encoders and decoders, it is possible to have different lengths for input and output sequences, generating representations (input sequences to vectors), and then generating sequences (a vector input mapped to a sequence). Sequence-to-sequence is a class of frameworks, and the specific models used by the encoder and decoder can be customized. For example, in machine translation, both the encoder and decoder can use LSTM. End-to-end models utilize the intermediate representation c, making the output depend only on the representation and the previously output sequence.

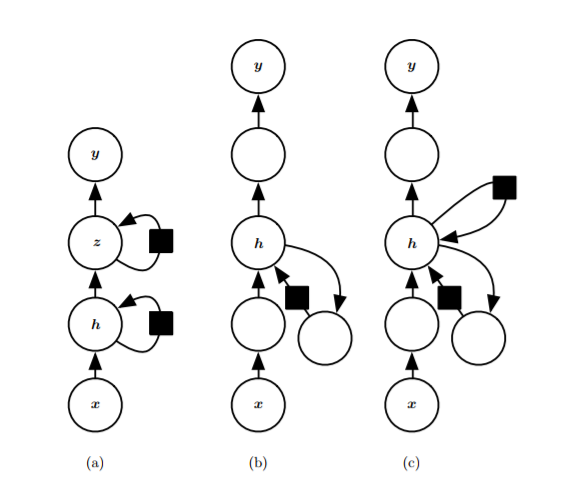
Deep RNN

• A. Deepen the cyclic state, decomposing it into multiple hierarchical groups, i.e., deepen horizontally (hidden layer updates within a single cycle are performed multiple times)
• Introducing a neural network between input and hidden, hidden to output, and hidden to hidden, i.e., deepening the hidden layer states not only horizontally (time steps) but also vertically (a single training).
• C. Introducing skip connections to alleviate the path elongation effect caused by deepening the network

Long-term dependency problem in RNN

• Long-term dependency problem: As models become deeper, they lose the ability to learn previous information
• Perform eigenvalue decomposition on the weight matrix, repeatedly perform linear transformations, which is equivalent to matrix power operations, and the eigenvalues are also subjected to power operations. Eigenvalues with a magnitude greater than 1 will explode, and those less than 1 will disappear. A severely deviated gradient value can lead to a gradient cliff (learning a very large update). If it has exploded, the solution is to use gradient clipping, using the direction of the calculated gradient but limiting the size to within a small step length.
• It is best to avoid gradient explosion. In recurrent neural networks, transformations between hidden layers do not introduce nonlinear transformations, which is equivalent to performing power operations on the weight matrix, causing eigenvalues to explode or vanish, and correspondingly, the gradients of long-term interactions become exponentially small. Ways to avoid this include introducing skip connections in the time dimension (adding edges over long time spans), introducing leaky units (setting linear self-connected units with weights close to 1), and removing edges over short time spans (retaining only edges over long time spans).

Gated RNN

- Addressing the long-term dependency problem using a method similar to the leaky unit, gated RNNs, including LSTM and GRU, were introduced.

• Leakage Unit (?): We apply an update to µ(t) for certain v values as µ(t) ← αµ(t−1) + (1−α)v(t), accumulating a moving average µ(t), where α is an example of a linear self-connection from µ(t−1) to µ(t). When α approaches 1, the moving average can remember information for a long time in the past, while when α approaches 0, information about the past is quickly discarded. The hidden unit µ with linear self-connection can simulate the behavior of the moving average. This hidden unit is called a leakage unit.

Long Short-Term Memory

• LSTM: makes the weights of the self-recurrent connections context-dependent (gated control of the weights of this recurrence)
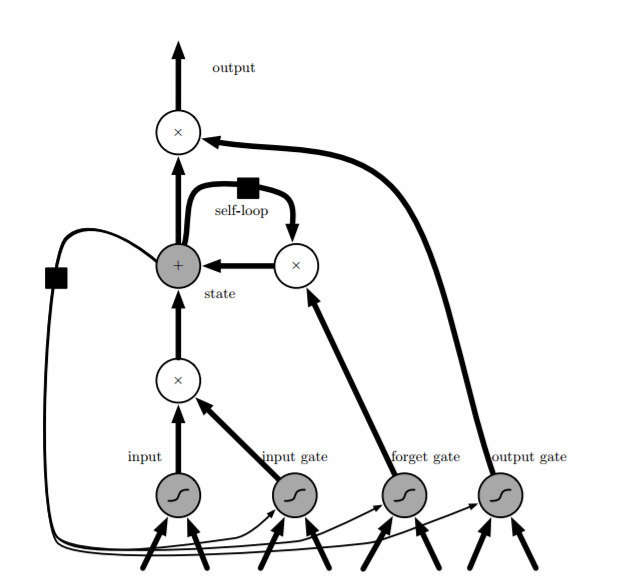
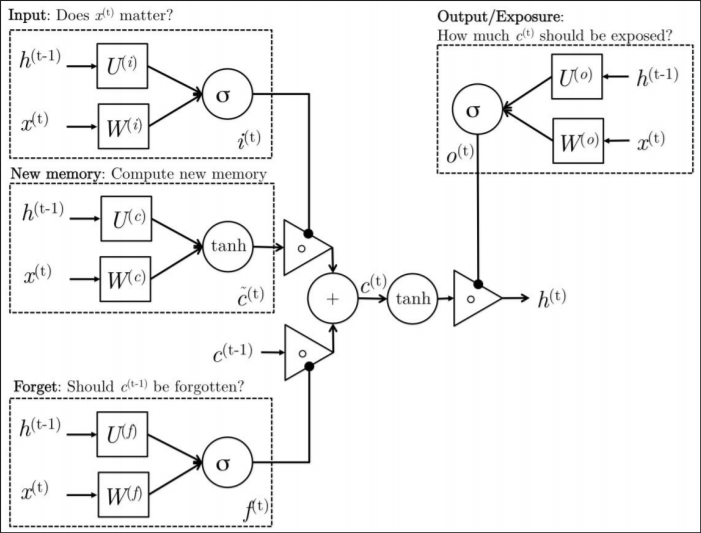
• LSTM modifies the hidden layer nodes (cells) in the ordinary RNN, with the internal structure as shown in the figure below:
• Visible in addition to the recurrent connections between cells in RNNs, there is an internal loop containing a forget gate control (how much to forget). The cell has an internal state s, which is different from the cell output h used for hidden layer updates between different time steps.
• All gate units have sigmoid nonlinearities, with input units being ordinary neurons that can use any nonlinear activation function.
• Three gates receive the same type of input, i.e., the current input x, the output of the cell at the previous time step h (not the internal state s), each having an independent weight matrix and bias. The outputs all pass through a sigmoid function to produce a value between 0 and 1, respectively representing the degree of memory of the current internal state s for the previous internal state, the degree of memory of the current internal state for the current input, and the degree of dependence of the current output on the current internal state of the cell.
• s: Updated internally based on two pieces of information: the previous internal state controlled by the forget gate, and the sum of the input controlled by the input gate and the cell output from the previous time step (not depicted in the figure?).
• Cell outputs h, the internal state overactivates the activation function, controlled by the output gate.
• Another more easily understandable figure:

Bidirectional LSTM

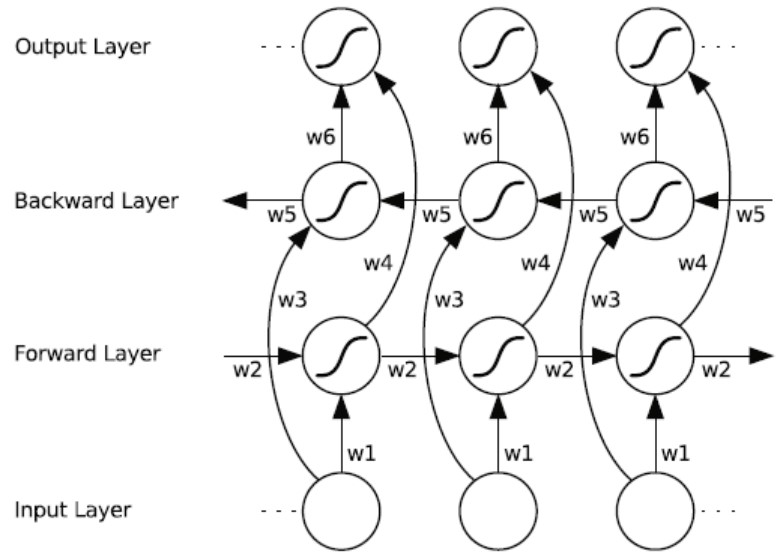
• As with bidirectional RNNs, each hidden layer node is an LSTM node, and there are no connections between the two hidden layer nodes in the bidirectional structure. Both hidden layers must be fully updated before the output layer can be computed, and the output at each time step depends on six weight matrices from w1 to w6.
• Because each output layer node receives the output of two hidden layer nodes, a processing step is required, and there are multiple ways to do this:
  • Direct Connection (concat)
  • Sum

Word embedding, Word2Vec

• Using the distributed representation of words (word embeddings or word vectors) to model natural language sequences, through the training of context-word pairs (one-hot vectors), a neural network is obtained, and the weight matrix from the input layer to the hidden layer is considered to contain all word vectors in the dictionary, i.e., the word vector matrix. At this point, by passing the individual one-hot word vectors through the neural network, a low-dimensional word embedding of this word can be obtained in the hidden layer with the help of the weight matrix (word vector matrix). Since word vectors are obtained as by-products of training with context-word pairs, the distances between word vectors in space have actual significance, i.e., words semantically related have vectors that are closer together. A problem with this generation method is the high dimensionality, because the output of the neural network is the word vector, which is reduced to a one-hot vector by softmax, representing the probability of each word. When the dictionary capacity is very large, this leads to a very large computational load in the final output layer. W2V is a practical scheme for generating word vectors, which optimizes the generation of word vectors based on the NLM model and solves the high-dimensional problem. It utilizes two optimization schemes:
• Hierarchical softmax: The output is no longer a probability vector of dictionary size, but a tree, with leaf nodes being words, internal nodes representing word groups, represented by conditional probabilities, and using a logistic regression model. W2V utilizes this model, eliminating the hidden layer, directly projecting the output of the projection layer into the tree, and improving the tree to a Huffman tree. Because the hidden layer is eliminated, W2V avoids large-scale matrix computations linearly related to the dictionary size from the projection layer to the hidden layer and from the hidden layer back to the output layer, but because the number of leaf nodes in the tree is still the same as the dictionary size, the final normalization computation of probabilities is still very costly.
• Important Sampling (?): This method reduces the computational load by reducing the gradients that need to be calculated during backpropagation. Each output word with the highest probability (positive phase) should contribute the most to the gradient, while the negative phase items with lower probabilities should contribute less. Therefore, instead of calculating the gradients for all negative phase items, a sampling of some is computed.
• Incomplete understanding of several simplification methods for the computation of softmax layers, to be improved. Recommended blog post: Technology | Series of Blogs on Word Embeddings Part 2: Comparison of Several Methods for Approximating Softmax in Language Modeling

Attention Mechanism

• In the seq2seq model, the information provided by the encoder is all compressed into an intermediate representation, i.e., the output of the hidden layer state at the last time step of the encoder, and the decoder decodes only based on this intermediate representation and the word decoded in the previous step. However, when there are many time steps in the encoder, the intermediate representation generally suffers from severe information loss, and to solve this problem, an attention mechanism is introduced.
• The actual performance of attention is to generate intermediate representations by weighted averaging over various time steps at the encoding end, rather than generating uniformly at the final step of the loop. The time steps at the encoding end with higher weights, which are referred to as the attention points, contribute more information to the decoding end.

前馈神经网络相关

• 数据维数很高时，样本空间容量可能远大于训练样本数目，导致维数灾难。

• 激活函数.用于表示神经网络中的非线性变换，没有激活函数而只有权重矩阵的话神经网络是线性变换的组合，依然是线性变换。利用非线性变换能提取出方便进行线性变换的特征，避免维数灾难(?)。

• Softmax和sigmoid的意义：具有最大熵，方便求导，万能近似定理（具有挤压性质）

• 隐藏层可使用激活函数ReLU，即整流线性，缺陷是不能使用梯度学习使函数激活为0的样本，因此发展了三种扩展：

  \[ g(z,\alpha)_i = max(0,z_i) + \alpha _i min(0,z_i) \]

  绝对值整流：右边系数为-1 渗漏整流：右边系数固定为一个较小值 参数化整流：系数放到模型中学习

反向传播

• 反向传播将输出的偏差通过梯度计算出参数的更新值，从输出层往输入层一层一层更新参数，传播的是上一层用到的梯度，利用向量的微积分链式法则。 每一层更新量=本层Jacobian矩阵*上一层梯度。
• 神经网络中的反向传播： 初始化梯度表 最后一层输出对输出求梯度，因此初始值为1 从后往前循环，本层的梯度表是本层Jacobian矩阵和上一层梯度表相乘（即链式求导）。 本层使用上一层的梯度表进行计算，并存储，避免链式法则中的多次重复计算。

RNN循环神经网络

RNN

• 特点：所有的隐藏层共享参数，将隐藏层作为状态变量，方便参数化。

• 用双曲正切作为隐藏层激活函数

• 输入x，x过权重矩阵经隐藏层激活后得到h，h过权重矩阵输出o，代价L，o经输出激活后得到y

• 基本结构（展开和非展开）：

• 几种变式：

  • 每一个时间步均有输出，隐藏层之间有循环连接：
  • 每一个时间步均有输出，输出与隐藏层之间有循环连接：
  • 读取整个序列后产生单个输出：

• 普通的前向传播，softmax处理输出，负对数似然作为损失函数，通过时间反向传播代价过大。 前馈过程：

  \[ \alpha ^{(t)} = b + Wh^{(t-1)} + Ux^{(t)}, \\ h^{(t)} = tanh(a^{(t)}), \\ o^{(t)} = c + Vh^{(t)}, \\ y^{(t)} = softmax(o^{(t)}) \\ \]

  代价函数：

  \[ L(\{ x^{(1)} , ... , x^{(\tau)}\},\{ y^{(1)} , ... , y^{(\tau)}\}) \\ =\sum _t L^{(t)} \\ = - \sum _t log p_{model} (y^{(t)}|\{ x^{(1)} , ... , x^{(\tau)}\}) \\ \]

• 改为第二种RNN，使用输出到隐藏层的循环，消除了隐藏层到隐藏层的循环，解耦并行(?)，使用导师驱动模型（用正确输出训练到隐藏层的循环网络W，测试时用贴近正确输出的实际输出经过网络W） 导师驱动模型：

双向RNN

• 考虑对未来信息的依赖，相当于两类隐藏层结合在一起

序列到序列

• 采用编码器和解码器，可以让输入输出序列长度不同，生成表示（输入序列到向量），再由表示生成序列（一个向量输入映射到序列）。序列到序列是一类框架，编码解码器使用的具体模型可以自定。例如机器翻译，编码器和解码器都可以用LSTM。端到端的模型利用中间表示c，使得输出仅依赖于表示和之前输出的序列。

深度RNN

• A.将循环状态加深，分解为多个具有层次的组，即横向加深（一次循环内隐藏层更新经过多次状态）
• B.在输入到隐藏，隐藏到输出，隐藏到隐藏之间引入神经网络，即对隐藏层状态不仅横向（时间步）加深，而且纵向（一次训练）加深
• C.引入跳跃连接来缓解加深网络后导致的路径延长效应

RNN中的长期依赖问题

• 长期依赖问题：模型变深，失去了学习到先前信息的能力
• 对权重矩阵做特征值分解分解，反复做线性变换，相当于矩阵幂运算，特征值也相应做幂运算，特征值量级大于1会爆炸，小于1会消失。梯度值严重偏离会导致梯度悬崖（学习到一个非常大的更新），如果已经爆炸，解决办法是使用梯度截断，使用计算出的梯度的方向但大小限制在一个小步长以内。
• 最好是避免梯度爆炸。在循环网络中，隐藏层到隐藏层之间的变换没有引入非线性变换，即相当于对权重矩阵做幂运算，特征值会爆炸或者消失，相对应的长期相互作用的梯度值就会变得指数小。避免的办法包括引入时间维度的跳跃链接（添加长时间跨度的边）、引入渗漏单元（设置权重接近1的线性自连接单元）、删除短时间跨度的边（只保留长时间跨度的边）

门控RNN

-用类似渗漏单元的方法解决长期依赖问题，引入了门控RNN，包括LSTM和GRU。

• 渗漏单元(?)：我们对某些 v 值应用更新 µ (t) ← αµ(t−1) + (1−α)v (t) 累积一个滑动平均值 µ (t)，其中 α 是一个从 µ (t−1) 到 µ (t) 线性自连接的例子。当 α 接近 1 时，滑动平均值能记住过去很长一段时间的信息，而当 α 接近 0，关于过去的信息被迅速丢弃。线性自连接的隐藏单元µ可以模拟滑动平均的行为。这种隐藏单元称为渗漏单元。

LSTM

• LSTM：使自循环的权重视上下文而定（通过门控控制此循环的权重）
• LSTM将普通RNN中的隐藏层节点（细胞）改造，内部结构如下图：
• 可见除了RNN中细胞之间的循环之外，细胞内包含一个遗忘门控制（遗忘多少）的内循环。细胞有一个内部状态s，不同于不同时间步之间隐藏层更新用到的细胞输出h
• 所有门控单元具有sigmoid非线性，输入单元是普通神经元，可以用任意非线性激活函数。
• 三个门接受相同类型的输入，即当前输入x，前一时间步细胞输出（而不是细胞内部状态s）h，各自有独立的权重矩阵和偏置，输出都过一个sigmoid输出一个（0,1)之间的值，分别代表当前内部状态s对上一时间布内部状态的记忆程度、当前内部状态对当前输入的记忆程度、当前输出对当前细胞内部状态的依赖程度。
• 内部状态更新s：根据两部分信息更新：由遗忘门控制的上一步内部状态，由输入门控制的输入和上一时间步细胞输出（未在图中画出？）之和。
• 细胞输出h，内部状态过激活函数，由输出门控制。
• 另一张更好理解的图：

双向LSTM

• 同双向RNN，每一个隐藏层节点都是lstm节点，且双向的两个隐藏层节点之间没有连接，需要将两个隐藏层全部更新完才能计算输出层，每一时间步的输出依赖w1到w6共6个权重矩阵。
• 因为每一个输出层节点接受两个隐藏层节点的输出，需要做一个处理，有多种方式：
  • 直接连接(concat)
    
  • 求和

词嵌入、Word2Vec

• 使用词的分布式表示（词嵌入或词向量）对自然语言序列建模，通过上下文-单词对(one-hot向量)的训练，得到神经网络，并将输入层到隐藏层的权重矩阵看成包含了词典中所有单词词向量，即词向量矩阵。此时再将单独的one-hot词向量通过神经网络，就可以借助权重矩阵（词向量矩阵）在隐藏层中得到这个词的低维词嵌入。因为词向量是通过上下文-单词对进行训练得到的副产品，因此这种词向量在空间上的距离具有实际意义，即语义上有联系的单词向量之间的距离较近。这种生成方法的一个问题是高维生成，因为神经网络中输出是词向量过softmax还原成一个one-hot向量，代表各个词的概率，词典容量非常大时会导致最后输出层计算量非常大。W2V是具有实用价值的产生词向量的方案，在使用NLM模型产生词向量的基础上进行优化，解决了高维问题，它利用了两套优化方案：
• 分层softmax：输出不再是词典大小的概率向量，而是一棵树，叶子节点是单词，内部节点代表词的组别，用条件概率表示，使用逻辑回归模型。W2V利用这个模型，取消了隐藏层，直接将投影层输出到树中，并将树改进为哈夫曼树。因为取消了隐藏层，W2V避免了从投影层到隐藏层和从隐藏层还原到输出层中与词典大小成线性相关的大规模矩阵计算，但是因为树的叶子节点数依然和词典大小一样，最后归一化计算概率时依然开销很大。
• 重要采样(?)：此方法通过减少反向传播时需要计算的梯度来减少计算量。每一次输出概率最高的词（正相项）对梯度应该贡献最大，其余概率低的负相项贡献应该低，因此不对所有的负相项计算梯度，而是采样一部分计算。
• 没有完全理解计算softmax层的几种简化方式，待完善。推荐博文：技术 | 词嵌入系列博客Part2：比较语言建模中近似softmax的几种方法

注意力机制

• 在seq2seq模型中，编码端提供的信息全部压缩成一个中间表示，即编码器最后一个时间步的隐藏层状态输出，解码器只根据这个中间表示和上一次解码的词语进行解码，然而在编码端时间步很多的情况下，中间表示一般信息损失严重，为了解决这个问题引入注意力机制。
• 注意力的实际表现是对编码端的各个时间步加权平均生成中间表示，而不是统一在循环的最后一步生成。权重大的编码端时间步即所谓的注意力所在点，给予解码端更多的信息贡献。